Back to Vibrational Relationships - Derivation
A nitrogen molecule, N2, provides a good, simple, quantitative introduction to molecular vibration quantities. The MNDO method will be used mainly because it is very old and stable, and all the steps described here can be reproduced using any copy of MOPAC. Several different quantities will be used in this example. To assist in conversions, a set of conversion factors are useful.
The starting point will be the N2 molecule at its equilibrium distance, 1.1038 Ångstroms.
Data-set
The following dataset was used as the source for many of the numbers mentioned here. Keywords DFORCE, FMAT, LARGE, NOSYM, and NOREOR were used in order to provide expanded output, normally only FORCE would be used.
DFORCE MNDO FMAT LARGE NOSYM NOREOR Calculate the vibrational frequency of N2 N 0.00000000 +0 0.00000000 +0 0.00000000 +0 N 1.10380157 +1 0.00000000 +0 0.00000000 +0
Build the Hessian matrix
Hessian matrices for vibrational calculations are constructed using the gradients of the displaced Cartesian coordinates for each atom, and the following expression, for a description of how this is constructed, see Hessian matrix.
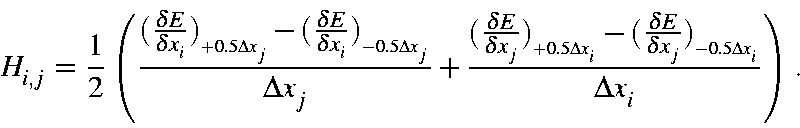
In this equation, Δxi = Δxj = 0.00833333 Å. This step-size was selected automatically, and similar step-size would work just as well. Only one matrix element, H(1,4), is important, this represents the N-N stretch along the "X" axis.
Four gradients are present in this equation, their values for Hessian element H(1,4) are:
| Gradient | Dist. N-N (Å) | Gradient (kcal mol-1 Å-1) | |
| 1 | (dE/dx1)@(+0.5Δx4) | 1.10796823 | -18.292733 |
| 2 | (dE/dx1)@(-0.5Δx4) | 1.09963491 | +18.832255 |
| 3 | (dE/dx4)@(+0.5Δx1) | 1.09963491 | -18.832815 |
| 4 | (dE/dx4)@(-0.5Δx1) | 1.10796823 | +18.292156 |
Ideally, gradients 1 and 4 should be the same, as should gradients 2 and 3, but because of numerical imprecision there are small differences. A 30% reduction in numerical imprecision can be achieved by averaging gradients 1 and 4, and 2 and 3.
Matrix element H(1,4) can then be calculated using these gradients, giving H(1,4) = -4455.175 kcal x mol-1 x Å-2
Convert to SI
Converting the Hessian from (kcal mol-1 Å-2) to (millidynes Å-1) involves multiplying the Hessian by a factor. This factor can be expressed variously as:
| Factor | = (J m-1 to millidynes) (kcal to Joules)/((Å to m)(Mole to molecule)) |
| = (108)(4184)/((10-10)(6.022
x 1023)) = 6.9477 x 10-3 |
When this is done, the matrix element becomes H(1,4) = -4455.175 x 6.9477 x 10-3 = -30.9520 millidynes x Å-1
Mass-weighting the Hessian
The final step in preparing the matrix for diagonalization involves mass-weighting. This operation is straightforward:
For all matrix elements:
| Hi,jm | = Hi,j x (Mi x Mj)-½ millidynes x Å-1 x amu-1 |
Nitrogen atoms have a mass of Mi = 14.0067 amu, so matrix element H(1,4) is:
| H1,4m | = -30.9520*(14.0067*14.0067)-½ |
| = -2.20980 millidynes x Å-1 x amu-1 |
Convert the mass-weighted Hessian into normal modes of vibration
When the mass-weighted Hessian is diagonalized, the result is a set of eigenvalues, εi, and associate eigenvectors, ψi. The eigenvectors are the coefficients of the wave-function that represents the normal modes of vibration, and form an orthonormal set. The eigenvalues represent the force constants for the modes divided by the effective mass. Nitrogen has only one non-trivial vibration, so:
| Eigenvalue ε1 of mass-weighted Hessian | |
| ε1 | = 4.4196 millidynes x Å-1 x amu-1 |
and the eigenvector: ψ1 is (0.7071) x (N1(x) - N2(x)). This represents the N - N stretch mode.
Recap of force constant and reduced mass
Eigenvalues, εi, of the mass-weighted Hessian are related to the force-constant, ki, and reduced mass, μi, for a normal mode of vibration by:
εi = ki/μi
Calculation of the Reduced Mass for the N-N stretch
Given the normal mode eigenvector, the reduced mass for the vibration can be calculated from:
μi = ΣA((ψi(A)(x))2 + (ψi(A)(y))2 + (ψi(A)(z))2)2 MA amu
where "A" refers to atom A, and "x", "y", and "z" refer to the respective Cartesian coordinate of atom "A".
For the vibration in N2, this sum is:
| μ1 | = ((0.7071)2)2 x 14.0067 + ((-0.7071)2)2 x 14.0067 |
| = 7.00335 amu | |
| = 1.16294 x 10-23 g |
Calculation of the Force Constants for the N-N stretch
Given ε1 and μ1, the force constant, k1 is:
| k1 | = 4.4196 x 7.00335 millidynes x Å-1 x amu-1 x amu |
| = 30.952 millidynes x Å-1 | |
| = 30.952 x 105 dynes x cm-1 | |
Convert eigenvalues to wavenumbers (frequencies) in reciprocal centimeters
The eigenvalues are then converted into vibrational frequencies, νi, in cm-1 via:
| νi | = 1/(2πc) x (N x 105 x ε)½ |
| = 1/(2 x 3.1416 x 2.9979 x 1010) x (6.022
x 1028 x 4.4196)½ |
|
| = 1.3028 x 103 x εi½ | |
| = 2738.8 cm-1 |
Here, "c" is in centimeters per second, N is in moles, and ε is in millidynes x Å-1 x amu-1
Convert wavenumbers to period of oscillation (T) in femtoseconds
The period for a molecular vibration is normally given in femtoseconds, fs; one femtosecond is 10-15 of a second. The conversion from wavenumber to period is given by:
| T | = 1015 /( c x ν) |
| = 1015 / (2.9979 x 1010 x 2738.8) | |
| = 12.179 fs | |
| = 12.179 x 10-15 s |
Convert wavenumbers to Angular Frequency, ω
Angular frequency is the angular displacement per second, or 2π/T:
| ω | = 2 x 3.1416/(12.179 x 10-15) |
| = 5.1589 x 1014 s-1 |
Convert frequency into kcal/mol
| ν1 (kcal mol-1) | = ν1(cm-1) x N x h x c x (ergs per kcal)-1 |
| = 2738.8 x 6.022 x 1023 x 6.626 x 10-27 x 2.9979 x 1010 x (4.184 x 1010) -1 | |
| = 2738.8 x 2.859 x 10-3 | |
| = 7.830 kcal x mol-1 |
| ν1 | (erg)= (ν1(cm-1) x h x c) |
| = 2738.8 x 6.626 x 10-27 x 2.9979 x 1010 | |
| = 2738.8 x 1.9864 x 10-16 | |
| = 5.4404 x 10-13 erg | |
| = 5.4404 x 10-20 J |
Zero point energy
The zero-point energy of a polyatomic molecule is the sum of the zero-point energies of all its normal modes. The zero-point energy of a normal mode is half of its vibrational energy. For N2, the vibration of 2738.8 cm-1, corresponds to an energy of 7.83 kcal mol-1, so its zero-point energy is 3.915 kcal mol-1.
Convert energy represented by frequency into velocity of the atoms
The starting point for this operation is the familiar E = ½mv2.
For this operation, the cgs system will be used. Rearranging E = ½mv2
gives the velocity, v = (2E/m)½. At this point, E is the energy in
ergs per mole, and "m" is the reduced mass of the vibration in amu. These
quantities can be re-worded as ergs per molecule and reduced mass in grams.
Expanding and solving for the velocity gives:
| v | = (2E/m)½ |
| = (2 x (4.184 x 1010 x ν1) x μ1-1)½ | |
| = (2 x (4.184 x 1010 x 7.830 x 7.00335-1)½ | |
| = 3.0587 x 105 cm x s-1 |
This velocity can be split into velocity per atom, vA, using the vibrational wavefunction, ψi. First, the wavefunction must be re-normalized so that the total motion is 1.0 Ångstroms. This is done by dividing the coefficients for each atom by the square-root of the atomic mass:
ψiA' = ψiA x mA-½
Then re-normalizing using a normalization factor N,
N = (ΣA (ψiA'(x)2 + ψiA'(y)2 + ψiA'(z)2 )½)-1
to give:
ψi" = N x ψi'
Finally, the starting velocity of each atom can be calculated from:
vA = v x ψi"(A)
For nitrogen, the wavefunction from the mass-weighted Hessian was ψ1 = 0.7071 x N1(x) - 0.7071 x N2(x). After re-normalizing, this becomes ψ1" = 0.5 x N1(x) - 0.5 x N2(x), and the velocity of each atom becomes:
v1 = 1.52935 x 105 cm x sec-1
and
v2 = -1.52935 x 105 cm x sec-1
in the "x" direction. This calculation is a bit tedious, but an easier way to obtain the same result is to examine the output file from a DRC calculation, see below.
Travel
In a molecular vibration the system starts at the energy minimum, then each atom moves along a path defined by the normal mode eigenvector. At the turning point - the point where atomic motion stops - the sum of the distances that the atoms are from their original position is the travel distance. In the case of the N2 molecule, this is the distance from N1 to its equilibrium position plus the distance of N2 from its equilibrium position. This quantity can also be calculated using the energy of the vibration and the force constant for the mode. The cgi system is used in this calculation:
| ν1 | = ½ k Δx12 |
| Δx1 | = (2ν1/k1)½ |
| = (2 x 5.4405 x 10-13 x (30.952 x 105)-1)½ | |
| = (3.5154 x 10-19)½ | |
| = 0.5929 x 10-9 cm | |
| = 0.05929 Å |
The travel can be partitioned into contributions from individual atoms using the same strategy as that used in the previous section on velocity, but a faster way to obtain the same result is to examine the output file from a DRC calculation, see below..
Maximum acceleration
Acceleration is at a maximum at the turning point of the energy in a molecular vibration. At that point, the geometry is at its maximum distortion from the equilibrium. Assuming simple harmonic motion, then the acceleration, a, is given by:
a = -(2πf)2x
where f = frequency in hertz. = 1/(12.17 *10-15) = 8.22 x 1013 hertz, and x, the travel or distance from the geometry at the energy minimum, is a = 0.05929 Å = 5.929 x 10-10 cm. Solving this gives:
a = 2.667 x 1023 x 5.929 x 10-10 cm x s-2 = 1.581 x 1014 cm x s-2
This acceleration can be compared with the acceleration due to gravity. 1G = 9.807 x 102 cm x s-2, therefore the maximum acceleration is 1.612 x 1011 G
An animation of a single complete vibration of the N-N stretch normal mode and the output can be used in verifying many of the calculations shown here.
To reproduce this cycle, use the following data-set:
IRC=1 DRC T-priority large bigcycles=1 mndo HTML N2 one complete vibrational cycle (To see N-N distance, click on "Script" at the bottom.) N N 1.10380157 1Notes
The step-size used in this animation is 0.1 femtosecond or 1 x10-16 s.
Small differences can be seen when the calculated results and the equivalent
results obtained from the animation or output are compared. Some of these
are due to round-off, and some are due to the difference between simple harmonic
motion and the calculated trajectory, but in general the agreement is very good,
indicating that the trajectory was almost simple harmonic.
|
Comparison of Quantities calculated here with those in the animation or output |
||||
| Quantity | Units | Calc'd | Animation and output | |
| Period of oscillation | femtoseconds | 12.17 | 12.2 | |
| Energy of vibration | kcal mol-1 | 7.83 | 7.83 | |
| Travel | Ångstroms | 0.0593 | 0.0596 | |
| Initial velocity | cm s-1 | 3.0587 x 105 | 3.0585 x 105 † | |
| †: Output only. | ||||