The transition state for many reactions can be easily obtained by simple mapping out the path resulting from steadily increasing or decreasing an interatomic distance. For example, the transition state for a hydrogen atom migrating from one carbon atom to the other in ethyl radical, CH3-CH2, can be generated by defining a "reaction path" consisting of the distance from the carbon atom of the CH2 group to one of the hydrogen atoms on the CH3 group, then steadily reducing this distance. At each point on this path, everything is optimized except, of course, the distance along the reaction path. As the distance is reduced, the energy will rise steadily until the transition state geometry is reached, then the energy will either start descending or it will descend suddenly. If the energy drops suddenly, it is always accompanied by a significant change in geometry. This unwanted effect can make locating the transition state a difficult task.
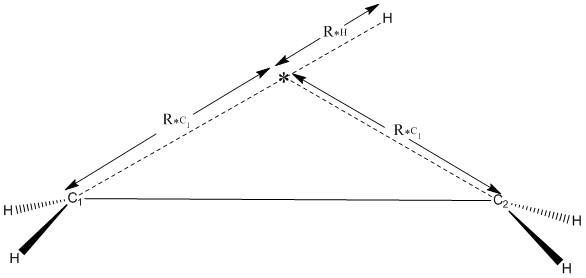
An alternative, ideally suited for motion involving a single atom, for example a hydrogen migration, is to re-define the reaction path in terms of the distances from the migrating atom to both the acceptor and donor atoms. An example for the hydrogen migration in the ethyl radical is shown in the figure. In this method, a dummy atom, shown here as an asterisk, *, is defined as being equidistant from the donor and acceptor atoms. This involved defining the position of the dummy atom using the distance, R*C1, to to the donor atom, and using the same distance in defining the position of the acceptor atom. The position of the moving atom, in this case a hydrogen atom, is then defined by a "reaction path" distance, R*H, from the dummy atom.

|
The position of the dummy atom, the distance to the acceptor atom, and the position of the migrating atom all need to be defined in internal coordinates. Because the acceptor atom distance is defined as an internal coordinate, its other two coordinates must also be in internal coordinates. The dummy atom's position has three degrees of freedom, its distance from the donor atom its angle and its dihedral. The acceptor atom has two degrees of freedom, its angle and dihedral; its distance from the dummy atom is symmetry defined, so that is not a degree of freedom.
The position of the migrating atom is defined by its distance from the dummy atom. This is the only variable it has. The migrating atom's angle is fixed at 180°and involves the dummy atom and the donor atom. At this angle, the dihedral is meaningless, so this can be defined as 0°and can be referenced to any nearby atom. This arrangement means that the migrating atom, the dummy atom, and the donor atom are always in a straight line.
In the reaction path, the adjustable quantity is the dummy atom - migrating atom distance. Given that, in most reactions the transition state geometry involves the migrating atom being between the donor and acceptor atoms, a suitable starting point for the reaction would be that R*H = -0.5 Ångstroms. If the path from there to R*H = 0.5 Ångstroms were to be mapped out, it's likely that the transition state geometry would be seen in a plot of energy versus path. If it's not seen, then that same plot could be used in deciding whether to extend the starting point of the path or the ending point.
Using a dummy atom might appear to increase the number of geometric parameters, i.e., the number of degrees of freedom. In fact, this doesn't happen. Recall that the acceptor atom loses one degree of freedom, the distance, because that is defined to be the same as the donor - hydrogen distance. The migrating atom loses two degrees of freedom, its angle and dihedral, so the loss of these three degrees exactly compensates for the three new degrees introduced by the dummy atom.
Given that the number of degrees of freedom is correct, it might appear that there is still some limitation on the position of the moving atom. In practice, and provided the contained angle at both the donor and acceptor atoms is less than 90°, a condition that is always true in practice, there are no limits on the position of the moving atom. It can even be on the straight line connecting the donor and acceptor atoms, at which point the dummy atom is also on the same line.
Worked examples of the use of this technique can be examined by downloading the zip files.
| Animation of reaction | ZIP file | Description | ||
| CH3I + F(-) ⇔I(-) + CH3F | CH3I + F(-) | SN2 reaction in aqueous media | ||
| CH3CHCH3 ⇔ CH3CH2CH2 | CH3CHCH3 | Hydrogen atom migration | ||
|
Reaction path [HCO-CH-CH3]- + [C5H5N-CH3]+ ⇔ HCO-CH=CH2 + C5H6N-CH3 |
MODIFIED REACTION PATH for Hydride transfer |
Hydride transfer from a methyl group on propionaldehyde anion to the para or C4 carbon on the pyridinium cation. This reaction, although interesting, was particularly difficult to model. |