Hessian matrix in FORCE calculations

The Hessian matrix is the matrix of second derivatives of the energy with respect to geometry. The most important Hessian is that used in the FORCE calculation. Normal modes are expressed as Cartesian displacements, consequently the Hessian is based on Cartesian rather than internal coordinates. See also Vibrational Relationships - Derivation.

Although first derivatives are relatively easy to calculate, second derivatives are not. The simplest, although not an elegant, way to calculate [73] second derivatives is to calculate first derivatives for a given geometry, then perturb the geometry, do an SCF calculation on the new geometry, and re-calculate the derivatives. The second derivatives can then be calculated from the difference of the two first derivatives divided by the step size. This method, which is used in the EigenFollowing routine, is called "single-sided" derivatives.

The Hessian is quite sensitive to geometry, and should only be evaluated at stationary points. Because of this sensitivity, "double-sided" derivatives are used.

Calculation of the Hessian matrix

The elements of the Hessian are defined as:
\begin{displaymath}H_{i,j} = \frac{\delta^2E}{\delta x_i\delta x_j} \end{displaymath}

and are generated by use of finite displacements, that is, for each atomic coordinate xi, the coordinate is first incremented by a small amount, ½Dxj, the gradients calculated, then the coordinate is decremented by Dxj and the gradients re-calculated. The second derivative is then obtained from the difference of the two derivatives and the step size:
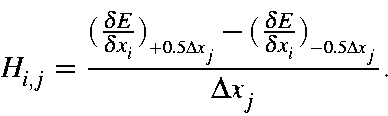
\begin{displaymath}H_{i,j} = \frac{(\frac{\delta E}{\delta x_i})_{_{+0.5\Delta x... ...rac{\delta E}{\delta x_i})_{_{-0.5\Delta x_j}}} {\Delta x_j}. \end{displaymath}

This is done for all 3N Cartesian coordinates. Because the Hessian is symmetric, that is, because Hi,j=Hj,i, the random errors that occur in the gradient calculation can be reduced (by a factor of (1/ 2)1/2) by re-defining the Hessian as:

Equation 1: Construct Hessian matrix

\begin{displaymath}H_{i,j} = \frac{1}{2}\left(\frac{(\frac{\delta E}{\delta x_i}... ...ta E}{\delta x_j})_{_{-0.5\Delta x_i}}} {\Delta x_i}\right). \end{displaymath}

A call to the energy - gradient function COMPFG will generate the gradients in kcal per mole per Ångstrom at a given geometry. The resulting second derivatives, in kcal per mole per Ångstrom squared, need to be converted into millidynes/Ångstrom (or its equivalent, 105 dynes/cm).  This involves an unusual conversion.  In the following expression, the input is in units of (kcal mol-1 Å-2) and the desired units are (millidynes Å-1), but dynes have the units of (J m-1), so only one of the input Å needs to be converted. 
 

The conversion from (J m-1) to millidynes is also unusual in that it involves two steps.  Expanded, this involves converting (J m-1) to dynes, followed by converting dynes to millidynes.  This involves the factors 105 times 103, so the total conversion factor is 108, as shown in the following expression:


This matrix represents the force constants for the system.  In order to calculate the vibrational frequencies it must first be mass-weighted:

\begin{displaymath}H^m_{i,j} = \frac{H_{i,j}}{\sqrt{M_i*M_j}}. \end{displaymath}

In this expression, Mi and Mj are the atomic weights in amu, so for a nitrogen molecule  Mi =  Mj  = 14.0067.

Diagonalization of this matrix yields eigenvalues, εi, from which the vibrational frequencies, νi can be calculated.  For simple harmonic motion involving a mass, m, and force-constant, k, the frequency, f, in cycles per second is given by:

f = 1/(2π) x (k/m)½ cycles per second

But, by convention, vibrational frequencies in UV-Visible spectroscopy are reported in reciprocal centimeters.  To convert from f to ν, f must be divided by the speed of light, c.

ν = f/c
  = 1/(2πc) x (k/m)½
  = 1/(2πc) x (εi)½ cm-1
   

At this point, some quantities are not in the correct units. The eigenvalues are in millidynes per Ångstrom per amu.  Before they can be used they must be converted into SI units, by using:
1 millidyne per Ångstrom = 102 J m-2,
Atomic mass units (amu) = 10-3 x N-1 kilograms. 

Combining these two factors together:

 Millidynes per Angstrom per amu = (102 x 103 x N) J m-2 kg-1 = (105 x N) Newton m-1 kg-1

Once this is done, the frequency in cm-1 can be calculated:

ν  = 1/(2πc)(105 x N x ε)½
  = 1/(2 x 3.1416 x 2.9979 x 1010)) x (6.022 x 1028 x ε)½
  = 1302.79 x ε½ cm-1

The eigenvalue also represents the quantity (k/μ)1/2 , where k is the force constant and μ is the reduced mass, but further discussion of this will be left until later.