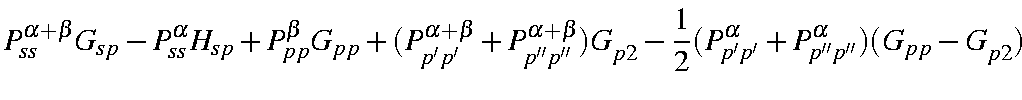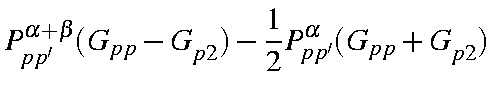One-center two-electron integrals

The MNDO, AM1, and MNDO-d one-center two-electron integrals are derived from experimental data on isolated atoms. Most were taken from Oleari's [54] work, but a few were obtained by optimization to fit molecular properties. The values of PM3 one-center two-electron integrals were optimized to reproduce experimental molecular properties.

For each atom there are a maximum of five one-center two-electron integrals. These are <ss|ss>, <ss|pp>, <sp|sp>, <pp|pp>, and <pp|p'p'>, where p and p' are two different p-type atomic orbitals. In the original formulation [55] there was a sixth integral, <pp'|pp'>, but it can be shown that this integral is related to two of the other integrals by:

<pp|p'p'> = 1/2( <pp|pp> - <pp|p'p'>)

Proof: If the molecular frame is rotated by 45$^\circ$ about the z axis the atomic bases mix thus:

R(45o)px = 0.7071(px + py)

R(45o)py = 0.7071(py - px)

R(45o)<pxpy|pxpy> = 1/4<(px + py)(py - px)|(px + py)(py - px)>

= 1/4(<px px|px px> + <py py|py py> - <px px|py py> - <py py|px px>)

 


or

R(45o)<pxpy|pxpy> = 1/2(<px px|px px>  -  <py py|px px>)

 

          For convenience these five integrals are given the following names:

<ss|ss> = Gss
<pp|pp> = Gpp
<sp|sp> = Hsp
<pp|pp> = Gpp
<pp|p'p'> = Gp2

Using these definitions, the two-electron one-center contributions to the Fock matrix become:
$\displaystyle F_{ss}^{\alpha}$ : $\displaystyle P_{ss}^{\beta}G_{ss}+(P_{p_x}^{\alpha+\beta}+P_{p_y}^{\alpha+\bet... ...alpha+\beta})G_{sp} -(P_{p_x}^{\alpha}+P_{p_y}^{\alpha}+P_{p_z}^{\alpha})H_{sp}$  
$\displaystyle F_{sp}^{\alpha}$ : $\displaystyle 2P_{sp}^{\alpha+\beta}H_{sp}-P_{sp}^{\alpha}(H_{sp}+G_{sp})$  
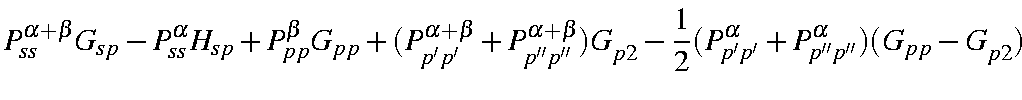$\displaystyle F_{pp}^{\alpha}$ : $\displaystyle P_{ss}^{\alpha+\beta}G_{sp}-P_{ss}^{\alpha}H_{sp}+ P_{pp}^{\beta}... ...beta})G_{p2} -\frac{1}{2}(P_{p'p'}^{\alpha}+P_{p  
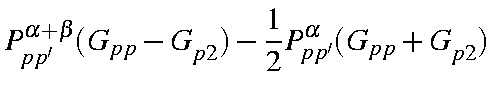$\displaystyle F_{pp'}^{\alpha}$ : $\displaystyle P_{pp'}^{\alpha+\beta}(G_{pp}-G_{p2}) -\frac{1}{2}P_{pp'}^{\alpha}(G_{pp}+G_{p2})$  

These expressions are common to all methods.