NDDO two-electron two-center integrals

In a local diatomic frame there are 22 unique two-electron two-center integrals for each pair of heavy (non-hydrogen) atoms. These are shown in Table 1.


 

Table 1:

 Two-Electron Two-Center Integrals (Local Frame)

1

<ss|ss>

12

<s  pσ|p<πpπ>

2

<ss|pππ>

13

<spσ|pσpσ> 

3

 <ss|pσpσ>

14

<ss|s pσ>

4

 <pπpπ|ss>

15

<pπpπ|s  pσ> 

5

<pσpσ|ss>

16

<pσpσ|s  pσ>

6

<pπpπ|pπpπ>

17

<s  pπ|s  pπ>

7

<pπpπ|pπ'pπ'  >

18

<s  pσ|s  pσ> 

8

<pπpπ|pσpσ>

19

<s  pπ| pπ pσ> 

9

<pσpσ|pπpπ>

20

<pπ pσ| s  pπ>  

10

<pσpσ|pσpσ> 

21

<pπ pσ|pπpσ>   

11

<s pσ|ss>

22

<pπpπ'|pπpπ'>


Each integral represents the energy of an electron density distribution (electron 1) arising from the product of the first two atomic orbitals interacting with the electron density distribution (electron 2), which in turn arises from the product of the second two atomic orbitals. Only if the first two atomic orbitals are the same and the second two are the same will the interaction energy have to be positive, in which case the integral represents an electron-electron repulsion term. In all other cases the sign of the integral value may be positive or negative.

With the exception of integral 22, all the integrals can be calculated using different techniques without loss of rotational invariance. That is, no integral depends on the value of another integral, except for number 22. As with the Hpp monocentric integral, it is easy to show that:

<pπpπ'|pπpπ'  > = 1/2(<pπpπ|pπpπ>  - <pπpπ|pπ'pπ'  >).

The electron density distributions are approximated by a series of point charges. There are four possible types of distribution. These are given in Table 2.

    

Table 2:

 Types of Electron Density Distribution

Monopole

Unit negative charge centered on the

(1 charge)

nucleus

 

 

Dipole

+1/2 charge located at position (x,y,z),

(2 charges)

-1/2 charge located at position (-x,-y,-z)

 

 

Linear Quadrupole

+1/2 charge located at the nucleus, -1/4 charge

(3 charges)

at positions (x,y,z) and at (-x,-y,-z)

 

 

Square Quadrupole

Four charges of magnitude +1/4, -1/4, +1/4

(4 charges)

and -1/4 forming a square centered on the nucleus.

These are used to represent the four types of atomic orbital products (Table 3).


 

Table 3:

 Density Distributions Arising from Pairs of Atomic Orbitals

Atomic Orbitals

Multipole Distribution

Number of Charges

<ss|

Monopole

1

<sp|

Dipole

2

<pp|

Monopole plus Linear Quadrupole

4

<pp'|

Square Quadrupole

4


Each two electron interaction integral is the sum of all the interactions arising from the charge distribution representing one pair of atomic orbitals with the charge distribution representing the second pair of atomic orbitals. Thus, in the simplest case, the <ss|ss> interaction is represented by the repulsion of two monopoles, while a <pπpπ|pπ' pπ'> , a much more complicated interaction, is represented by 16 separate terms, arising from the four charges representing the monopole and linear quadrupole on one center interacting with the equivalent set on the second center.

While the repulsion of two like charges is proportional to the inverse distance separating the charges, boundary conditions preclude using this simple expression to represent the interelectronic interactions. Instead, the interaction energy is approximated by:

All that remains is to specify functional forms for the terms c and A. c, the distance of a multipole charge from its nucleus, is a simple function of the atomic orbitals; in the case of a s-p product, this is a vector of length D1 Bohr pointing along the p axis, where

.

The principal quantum number is always the same in these methods for s and p orbitals on any given atom. The corresponding distances of the charges from the nucleus for the linear and square quadrupoles are 2D2 and 21/2D2 Bohr, respectively, where

.

Now that the distances of the charges from the nucleus have been defined, the upper boundary condition can be set. In the limit, when R=0.0, the value of the two-electron integral should equal that of the corresponding monocentric integral. Three cases can be identified:

1. A monopole-monopole interaction, in which case the integral must converge on Gss.
2. A dipole-dipole interaction, where the integral must converge on Hsp.
3. The quadrupole-quadrupole interaction where the integral must converge on Hpp.

For convenience, the GA terms are given special names. These are given in Table 4.    

Table 4:

 Additive Terms for Two-Electron Integrals

Multipole

Monocentric Equivalent

Name

Monopole

Gss

AM

Dipole

Hsp

AD

Quadrupole

Hpp =1/2(Gpp-Gp2)

AQ


In practice, 1/2(Gpp - Gp2) is used instead of Hpp. This eliminates any possibility of loss of rotational invariance due to an incorrect value of Hpp.

While AM is given simply by Gss/27.21, AD and AQ are complicated functions of one-center terms and the orbital exponents--recall that, in the limit, the associated charges are not all coincident. AD and AQ are solved iteratively. Given an initial estimate of AD of

begin{displaymath}AD = left[frac{H_{sp}}{27.21D^2_1}right]^{1/3},end{displaymath}

then, by iterating, an exact value of AD can be found. On iteration n the value of AD is given by

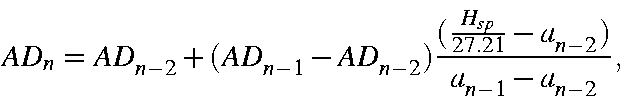
begin{displaymath}AD_n = AD_{n-2}+(AD_{n-1}-AD_{n-2})frac{(frac{H_{sp}}{27.21}-a_{n-2})}{a_{n-1}-a_{n-2}},end{displaymath}

where

an=1/2ADn-1/2(4D21+AD-2n)-1/2.

About 5 iterations are needed in order to get AD specified with acceptable accuracy.

Similarly, for AQ an initial estimate of $[frac{H_{pp}}{27.21(3D^4_2)}]^{1/5}$is made and, again, by iterating using

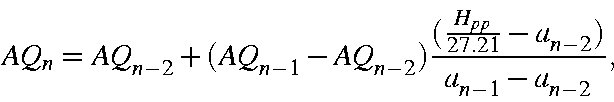
begin{displaymath}AQ_n = AQ_{n-2}+(AQ_{n-1}-AQ_{n-2})frac{(frac{H_{pp}}{27.21}-a_{n-2})}{a_{n-1}-a_{n-2}},end{displaymath}

where, now,

an=1/4AQn - 1/2(4D22+AQ-2n)-1/2 + 1/4(8D22+AQn-2)-1/2,

an exact value of AQ can be obtained. About 5 iterations are necessary.

Note that these equations are intrinsically unstable on finite-precision computers. The denominator (an-1 -an-2 ) rapidly becomes vanishingly small; this is, however, necessary in order to accurately define AD and AQ.

Order of storage of the two-electron integrals

Each two-electron integral can be represented by the symbol <ij|kl>, which represents the  integral are over atomic orbitals <psi_i(A), psi_j(A) (1/r12) psi_k(B) psi_l(B)>. The order of "ij" within any atom is: ss sx xx sy xy yy sz xz yz zz then the "d" orbitals, if present. For a s-p basis set there are 10 = (5*4)/2 two-atomic-orbital sets. For a s-p-d basis set there are 45 = (10*9)/2 two-atomic-orbital sets. The same is true for the "kl" set. So for a two atom system, CO, say, there would be 100 integrals for C with C, 100 for C with O, and 100 for O with O.

For the optimized CO molecule, using PM6, the complete set of 300 two-electron integrals is:

 <ss|ss> = Gss(C) <ss|xx> = Gsp(C)       <ss|yy>                         <ss|zz>      
 13.3355  0.0000 11.5281  0.0000  0.0000 11.5281  0.0000  0.0000  0.0000 11.5281  C with C (one center)
          <sx|sx> = Hsp(C)
  0.0000  0.7173  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000
                 <xx|xx> = Gpp(C)         <xx|yy> = Gp2(C)
 11.5281  0.0000 10.7783  0.0000  0.0000  9.4862  0.0000  0.0000  0.0000  9.4862
                          <sy|sy>
  0.0000  0.0000  0.0000  0.7173  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000
                                  <xy|xy> = Hpp(C) = 0.5*(Gpp(C) - Gp2(C)
  0.0000  0.0000  0.0000  0.0000  0.6461  0.0000  0.0000  0.0000  0.0000  0.0000
 11.5281  0.0000  9.4862  0.0000  0.0000 10.7783  0.0000  0.0000  0.0000  9.4862
  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.7173  0.0000  0.0000  0.0000
  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.6461  0.0000  0.0000
  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.6461  0.0000
 11.5281  0.0000  9.4862  0.0000  0.0000  9.4862  0.0000  0.0000  0.0000 10.7783

  8.7898  1.2038  9.0369  0.0000  0.0000  8.3085  0.0000  0.0000  0.0000  8.3085 C with O (two center)
 -0.8661 -0.2147 -1.0104  0.0000  0.0000 -0.6782  0.0000  0.0000  0.0000 -0.6782
  9.2177  1.0807  8.9159  0.0000  0.0000  8.5077  0.0000  0.0000  0.0000  8.5077
  0.0000  0.0000  0.0000  0.2241  0.2467  0.0000  0.0000  0.0000  0.0000  0.0000
  0.0000  0.0000  0.0000 -0.1865 -0.2586  0.0000  0.0000  0.0000  0.0000  0.0000
  8.3954  0.9975  8.3443  0.0000  0.0000  8.0901  0.0000  0.0000  0.0000  7.9903
  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.2241  0.2467  0.0000  0.0000
  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000 -0.1865 -0.2586  0.0000  0.0000
  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0499  0.0000
  8.3954  0.9975  8.3443  0.0000  0.0000  7.9903  0.0000  0.0000  0.0000  8.0901

 11.3040  0.0000 15.8074  0.0000  0.0000 15.8074  0.0000  0.0000  0.0000 15.8074 O with O (one center)
  0.0000  5.0108  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000 
 15.8074  0.0000 13.6182  0.0000  0.0000 10.3328  0.0000  0.0000  0.0000 10.3328
  0.0000  0.0000  0.0000  5.0108  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000
  0.0000  0.0000  0.0000  0.0000  1.6427  0.0000  0.0000  0.0000  0.0000  0.0000
 15.8074  0.0000 10.3328  0.0000  0.0000 13.6182  0.0000  0.0000  0.0000 10.3328
  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  5.0108  0.0000  0.0000  0.0000
  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  1.6427  0.0000  0.0000
  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  1.6427  0.0000
 15.8074  0.0000 10.3328  0.0000  0.0000 10.3328  0.0000  0.0000  0.0000 13.6182
The sequence of sub-matrices for a molecule with atoms in order A, B, C, D, is as follows:
AA
AB BB
AC BC CC
AD BD CD DD


For methane, with atoms in the order: C H1, H2, H3, H4, the number of two-electron integrals per atom pair would be:
CC 100 integrals
H1C 10 integrals
H1H1 1 integral
H2C 10 integrals
H2H1 1 integral
H2H2 1 integral
H3C 10 integrals
H3H1 1 integral
H3H2 1 integral
H3H3 1 integral
H4C 10 integrals
H4H1 1 integral
H4H2 1 integral
H4H3 1 integral
H4H4 1 integral

for a total of 150 integrals.  To see how these are related, run methane with HCORE and compare the two-electron matrix with the following integrals:

TWO-ELECTRON MATRIX IN HCORE (Methane)
 
 12.2300  0.0000 11.4700  0.0000  0.0000 11.4700  0.0000  0.0000  0.0000 11.4700    CC
  0.0000  2.4300  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000
 11.4700  0.0000 11.0800  0.0000  0.0000  9.8400  0.0000  0.0000  0.0000  9.8400
  0.0000  0.0000  0.0000  2.4300  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000
  0.0000  0.0000  0.0000  0.0000  0.6200  0.0000  0.0000  0.0000  0.0000  0.0000
 11.4700  0.0000  9.8400  0.0000  0.0000 11.0800  0.0000  0.0000  0.0000  9.8400
  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  2.4300  0.0000  0.0000  0.0000
  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.6200  0.0000  0.0000
  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.0000  0.6200  0.0000
 11.4700  0.0000  9.8400  0.0000  0.0000  9.8400  0.0000  0.0000  0.0000 11.0800
 
 9.0917  -0.6191  8.6000 -1.9992  0.2460  9.3181  0.0000  0.0000  0.0000  8.5239    H1C
12.8480                                                                             H1H1 
 
 9.0917  -0.7361  8.6315  0.9582 -0.1402  8.7063  1.7088 -0.2500  0.3254  9.1042    H2C   
 6.8458                                                                             H2H1 
12.8480                                                                             H2H2

 9.0917 -0.7361  8.6315  0.9582 -0.1402  8.7063 -1.7088   0.2500 -0.3254  9.1042    H3C  
 6.8458                                                                             H3H1  
 6.8458                                                                             H3H2 
12.8480                                                                             H3H3  

 9.0917  2.0912  9.3930  0.0827  0.0344  8.5252  0.0000  0.0000  0.0000  8.5239     H4C
 6.8458                                                                             H4H1                        
 6.8458                                                                             H4H2  
 6.8458                                                                             H4H3
12.8480                                                                             H4H4