Example of a "Walk" in k-space, from Program BZ
Diamond is both a very simple solid, consisting only of carbon atoms, and also a complicated solid, in that the band-structure is very complicated. As such, it is ideal for illustrating features of the Brillouin zone.
A good starting point for investigating the Brillouin zone of diamond is the simple data-set shown in Figure 1. Here, the geometry consists of the two carbon atoms of the primitive unit cell and the three translation vectors that define where the primitive unit cell is moved to by the
| Figure 1: Data-set for Diamond for use with MAKPOL | |
* * Data set for diamond, for use with BZ * MERS=(6,6,6) BCC let symmetry INT Diamond C C 1.545 1 0 0 0 0 1 Tv 1.784 0 54.73561 0 0 0 1 2 Tv 1.784 0 54.73561 0 120 0 1 2 3 Tv 1.784 0 54.73561 0 240 0 1 2 3 |
MERS=(6,6,6) Six unit cells in each of the three translational directions is sufficient to adequately represent the solid-state structure.
BCC Only unit cells where the sum of the cell indices is even are used.
LET For Brillouin zone work, atoms are not rearranged into the most aesthetically attractive form.
| Figure E1: Diamond Electronic
Band Structure Example of a "Walk" in k-space, from Program BZ |
 |
SYMMETRY Diamond has very high symmetry; keyword SYMMETRY can be used to both simplify the geometry optimization and to preserve the precise octahedral symmetry of the lattice.
INT The resulting geometry is to be in internal coordinates (these are better than Cartesian coordinates for high-symmetry solids.)
Names for data sets for MAKPOL need to be in the form MAKE_<name>.dat, so for diamond a suitable name would be MAKE_Diamond.dat. When MAKE_Diamond.dat is run using MAKPOL, a much larger data-set, Diamond.mop, is generated. This data-set contains some symmetry, but still has several geometric parameters flagged for optimization.
All angles and dihedral angles in diamond are, of course, fixed, so without loss of generality all angle and dihedral angle flags that were "1" can be changed to "0".
| Figure 2: Symmetrized data-set for Diamond for use with MOPAC | |
MERS=(6,6,6) BCC LET SYMMETRY Diamond C 0.000000 +0 0.000000 +0 0.000000 +0 C 1.545000 +1 0.000000 +0 0.000000 +0 1 C 2.958427 +0 100.024785 +0 0.000000 +0 2 1 C 1.545000 +0 100.024785 +0 180.000000 +0 3 2 1 C 2.958427 +0 100.024785 +0 180.000000 +0 4 3 2 C 1.545000 +0 100.024785 +0 180.000000 +0 5 4 3 C 1.544986 +0 109.470848 +0 -60.000000 +0 2 1 3 C 1.545000 +0 109.470848 +0 180.000000 +0 7 2 1 C 1.544986 +0 109.470848 +0 120.000000 +0 4 3 2 C 1.545000 +0 109.470848 +0 180.000000 +0 9 4 3 C 1.544986 +0 109.470848 +0 120.000000 +0 6 5 4 C 1.545000 +0 109.470848 +0 180.000000 +0 11 6 5 C 2.522957 +0 90.000000 +0 -90.000000 +0 7 2 1 C 1.545000 +0 90.000000 +0 -109.470848 +0 13 7 2 C 1.544986 +0 109.470848 +0 180.000000 +0 8 7 2 C 1.545000 +0 109.470848 +0 180.000000 +0 15 8 7 C 1.544986 +0 109.470848 +0 180.000000 +0 10 9 4 C 1.545000 +0 109.470848 +0 180.000000 +0 17 10 9 C 1.544986 +0 109.470848 +0 -90.000000 +0 14 13 7 C 1.545000 +0 109.470848 +0 180.000000 +0 19 14 13 C 1.544986 +0 109.470848 +0 180.000000 +0 16 15 8 C 1.545000 +0 109.470848 +0 180.000000 +0 21 16 15 C 1.544986 +0 109.470848 +0 180.000000 +0 18 17 10 C 1.545000 +0 109.470848 +0 180.000000 +0 23 18 17 C 2.522957 +0 90.000000 +0 -90.000000 +0 19 14 13 C 1.545000 +0 90.000000 +0 -109.470848 +0 25 19 14 C 1.544986 +0 109.470848 +0 180.000000 +0 20 19 14 C 1.545000 +0 109.470848 +0 180.000000 +0 27 20 19 C 1.544986 +0 109.470848 +0 180.000000 +0 22 21 16 C 1.545000 +0 109.470848 +0 180.000000 +0 29 22 21 C 1.544986 +0 109.470848 +0 -90.000000 +0 26 25 19 C 1.545000 +0 109.470848 +0 180.000000 +0 31 26 25 C 1.544986 +0 109.470848 +0 180.000000 +0 28 27 20 C 1.545000 +0 109.470848 +0 180.000000 +0 33 28 27 C 1.544986 +0 109.470848 +0 180.000000 +0 30 29 22 C 1.545000 +0 109.470848 +0 180.000000 +0 35 30 29 C 1.544986 +0 109.470848 +0 60.000000 +0 2 1 3 C 1.545000 +0 109.470848 +0 180.000000 +0 37 2 1 C 1.544986 +0 109.470848 +0 -120.000000 +0 4 3 2 C 1.545000 +0 109.470848 +0 180.000000 +0 39 4 3 C 1.544986 +0 109.470848 +0 -120.000000 +0 6 5 4 C 1.545000 +0 109.470848 +0 180.000000 +0 41 6 5 C 1.544986 +0 109.470848 +0 180.000000 +0 2 1 3 C 1.545000 +0 109.470848 +0 180.000000 +0 43 2 1 C 1.544986 +0 109.470848 +0 -60.000000 +0 8 7 2 C 1.545000 +0 109.470848 +0 180.000000 +0 45 8 7 C 1.544986 +0 109.470848 +0 -60.000000 +0 10 9 4 C 1.545000 +0 109.470848 +0 180.000000 +0 47 10 9 C 1.544986 +0 109.470848 +0 30.000000 +0 14 13 7 C 1.545000 +0 109.470848 +0 180.000000 +0 49 14 13 C 1.544986 +0 109.470848 +0 -60.000000 +0 16 15 8 C 1.545000 +0 109.470848 +0 180.000000 +0 51 16 15 C 1.544986 +0 109.470848 +0 -60.000000 +0 18 17 10 C 1.545000 +0 109.470848 +0 180.000000 +0 53 18 17 C 1.544986 +0 109.470848 +0 150.000000 +0 14 13 7 C 1.545000 +0 109.470848 +0 180.000000 +0 55 14 13 C 1.544986 +0 109.470848 +0 -60.000000 +0 20 19 14 C 1.545000 +0 109.470848 +0 180.000000 +0 57 20 19 C 1.544986 +0 109.470848 +0 -60.000000 +0 22 21 16 C 1.545000 +0 109.470848 +0 180.000000 +0 59 22 21 C 1.544986 +0 109.470848 +0 30.000000 +0 26 25 19 C 1.545000 +0 109.470848 +0 180.000000 +0 61 26 25 C 1.544986 +0 109.470848 +0 -60.000000 +0 28 27 20 C 1.545000 +0 109.470848 +0 180.000000 +0 63 28 27 C 1.544986 +0 109.470848 +0 -60.000000 +0 30 29 22 C 1.545000 +0 109.470848 +0 180.000000 +0 65 30 29 C 1.544986 +0 109.470848 +0 150.000000 +0 26 25 19 C 1.545000 +0 109.470848 +0 180.000000 +0 67 26 25 C 1.544986 +0 109.470848 +0 -60.000000 +0 32 31 26 C 1.545000 +0 109.470848 +0 180.000000 +0 69 32 31 C 1.544986 +0 109.470848 +0 -60.000000 +0 34 33 28 C 1.545000 +0 109.470848 +0 180.000000 +0 71 34 33 C 2.522957 +0 90.000000 +0 -90.000000 +0 43 2 1 C 1.545000 +0 90.000000 +0 -109.470848 +0 73 43 2 C 1.544986 +0 109.470848 +0 180.000000 +0 38 37 2 C 1.545000 +0 109.470848 +0 180.000000 +0 75 38 37 C 1.544986 +0 109.470848 +0 180.000000 +0 40 39 4 C 1.545000 +0 109.470848 +0 180.000000 +0 77 40 39 C 1.544986 +0 109.470848 +0 60.000000 +0 44 43 2 C 1.545000 +0 109.470848 +0 180.000000 +0 79 44 43 C 1.544986 +0 109.470848 +0 180.000000 +0 46 45 8 C 1.545000 +0 109.470848 +0 180.000000 +0 81 46 45 C 1.544986 +0 109.470848 +0 180.000000 +0 48 47 10 C 1.545000 +0 109.470848 +0 180.000000 +0 83 48 47 C 1.544986 +0 109.470848 +0 180.000000 +0 44 43 2 C 1.545000 +0 109.470848 +0 180.000000 +0 85 44 43 C 1.544986 +0 109.470848 +0 180.000000 +0 50 49 14 C 1.545000 +0 109.470848 +0 180.000000 +0 87 50 49 C 1.544986 +0 109.470848 +0 180.000000 +0 52 51 16 C 1.545000 +0 109.470848 +0 180.000000 +0 89 52 51 C 1.544986 +0 109.470848 +0 60.000000 +0 56 55 14 C 1.545000 +0 109.470848 +0 180.000000 +0 91 56 55 C 1.544986 +0 109.470848 +0 180.000000 +0 58 57 20 C 1.545000 +0 109.470848 +0 180.000000 +0 93 58 57 C 1.544986 +0 109.470848 +0 180.000000 +0 60 59 22 C 1.545000 +0 109.470848 +0 180.000000 +0 95 60 59 C 1.544986 +0 109.470848 +0 180.000000 +0 56 55 14 C 1.545000 +0 109.470848 +0 180.000000 +0 97 56 55 C 1.544986 +0 109.470848 +0 180.000000 +0 62 61 26 C 1.545000 +0 109.470848 +0 180.000000 +0 99 62 61 C 1.544986 +0 109.470848 +0 180.000000 +0 64 63 28 C 1.545000 +0 109.470848 +0 180.000000 +0 101 64 63 C 1.544986 +0 109.470848 +0 60.000000 +0 68 67 26 C 1.545000 +0 109.470848 +0 180.000000 +0 103 68 67 C 1.544986 +0 109.470848 +0 180.000000 +0 70 69 32 C 1.545000 +0 109.470848 +0 180.000000 +0 105 70 69 C 1.544986 +0 109.470848 +0 180.000000 +0 72 71 34 C 1.545000 +0 109.470848 +0 180.000000 +0 107 72 71 C 1.544986 +0 109.470848 +0 150.000000 +0 74 73 43 C 1.545000 +0 109.470848 +0 180.000000 +0 109 74 73 C 1.544986 +0 109.470848 +0 180.000000 +0 76 75 38 C 1.545000 +0 109.470848 +0 180.000000 +0 111 76 75 C 1.544986 +0 109.470848 +0 180.000000 +0 78 77 40 C 1.545000 +0 109.470848 +0 180.000000 +0 113 78 77 C 1.544986 +0 109.470848 +0 -90.000000 +0 74 73 43 C 1.545000 +0 109.470848 +0 180.000000 +0 115 74 73 C 1.544986 +0 109.470848 +0 180.000000 +0 80 79 44 C 1.545000 +0 109.470848 +0 180.000000 +0 117 80 79 C 1.544986 +0 109.470848 +0 180.000000 +0 82 81 46 C 1.545000 +0 109.470848 +0 180.000000 +0 119 82 81 C 1.544986 +0 109.470848 +0 60.000000 +0 86 85 44 C 1.545000 +0 109.470848 +0 180.000000 +0 121 86 85 C 1.544986 +0 109.470848 +0 180.000000 +0 88 87 50 C 1.545000 +0 109.470848 +0 180.000000 +0 123 88 87 C 1.544986 +0 109.470848 +0 180.000000 +0 90 89 52 C 1.545000 +0 109.470848 +0 180.000000 +0 125 90 89 C 1.544986 +0 109.470848 +0 180.000000 +0 86 85 44 C 1.545000 +0 109.470848 +0 180.000000 +0 127 86 85 C 1.544986 +0 109.470848 +0 180.000000 +0 92 91 56 C 1.545000 +0 109.470848 +0 180.000000 +0 129 92 91 C 1.544986 +0 109.470848 +0 180.000000 +0 94 93 58 C 1.545000 +0 109.470848 +0 180.000000 +0 131 94 93 C 1.544986 +0 109.470848 +0 60.000000 +0 98 97 56 C 1.545000 +0 109.470848 +0 180.000000 +0 133 98 97 C 1.544986 +0 109.470848 +0 180.000000 +0 100 99 62 C 1.545000 +0 109.470848 +0 180.000000 +0 135 100 99 C 1.544986 +0 109.470848 +0 180.000000 +0 102 101 64 C 1.545000 +0 109.470848 +0 180.000000 +0 137 102 101 C 1.544986 +0 109.470848 +0 180.000000 +0 98 97 56 C 1.545000 +0 109.470848 +0 180.000000 +0 139 98 97 C 1.544986 +0 109.470848 +0 180.000000 +0 104 103 68 C 1.545000 +0 109.470848 +0 180.000000 +0 141 104 103 C 1.544986 +0 109.470848 +0 180.000000 +0 106 105 70 C 1.545000 +0 109.470848 +0 180.000000 +0 143 106 105 C 2.522957 +0 90.000000 +0 -90.000000 +0 115 74 73 C 1.545000 +0 90.000000 +0 -109.470848 +0 145 115 74 C 1.544986 +0 109.470848 +0 180.000000 +0 110 109 74 C 1.545000 +0 109.470848 +0 180.000000 +0 147 110 109 C 1.544986 +0 109.470848 +0 180.000000 +0 112 111 76 C 1.545000 +0 109.470848 +0 180.000000 +0 149 112 111 C 1.544986 +0 109.470848 +0 60.000000 +0 116 115 74 C 1.545000 +0 109.470848 +0 180.000000 +0 151 116 115 C 1.544986 +0 109.470848 +0 180.000000 +0 118 117 80 C 1.545000 +0 109.470848 +0 180.000000 +0 153 118 117 C 1.544986 +0 109.470848 +0 180.000000 +0 120 119 82 C 1.545000 +0 109.470848 +0 180.000000 +0 155 120 119 C 1.544986 +0 109.470848 +0 180.000000 +0 116 115 74 C 1.545000 +0 109.470848 +0 180.000000 +0 157 116 115 C 1.544986 +0 109.470848 +0 180.000000 +0 122 121 86 C 1.545000 +0 109.470848 +0 180.000000 +0 159 122 121 C 1.544986 +0 109.470848 +0 180.000000 +0 124 123 88 C 1.545000 +0 109.470848 +0 180.000000 +0 161 124 123 C 1.544986 +0 109.470848 +0 60.000000 +0 128 127 86 C 1.545000 +0 109.470848 +0 180.000000 +0 163 128 127 C 1.544986 +0 109.470848 +0 180.000000 +0 130 129 92 C 1.545000 +0 109.470848 +0 180.000000 +0 165 130 129 C 1.544986 +0 109.470848 +0 180.000000 +0 132 131 94 C 1.545000 +0 109.470848 +0 180.000000 +0 167 132 131 C 1.544986 +0 109.470848 +0 180.000000 +0 128 127 86 C 1.545000 +0 109.470848 +0 180.000000 +0 169 128 127 C 1.544986 +0 109.470848 +0 180.000000 +0 134 133 98 C 1.545000 +0 109.470848 +0 180.000000 +0 171 134 133 C 1.544986 +0 109.470848 +0 180.000000 +0 136 135 100 C 1.545000 +0 109.470848 +0 180.000000 +0 173 136 135 C 1.544986 +0 109.470848 +0 60.000000 +0 140 139 98 C 1.545000 +0 109.470848 +0 180.000000 +0 175 140 139 C 1.544986 +0 109.470848 +0 180.000000 +0 142 141 104 C 1.545000 +0 109.470848 +0 180.000000 +0 177 142 141 C 1.544986 +0 109.470848 +0 180.000000 +0 144 143 106 C 1.545000 +0 109.470848 +0 180.000000 +0 179 144 143 C 1.544986 +0 109.470848 +0 150.000000 +0 146 145 115 C 1.545000 +0 109.470848 +0 180.000000 +0 181 146 145 C 1.544986 +0 109.470848 +0 180.000000 +0 148 147 110 C 1.545000 +0 109.470848 +0 180.000000 +0 183 148 147 C 1.544986 +0 109.470848 +0 180.000000 +0 150 149 112 C 1.545000 +0 109.470848 +0 180.000000 +0 185 150 149 C 1.544986 +0 109.470848 +0 -90.000000 +0 146 145 115 C 1.545000 +0 109.470848 +0 180.000000 +0 187 146 145 C 1.544986 +0 109.470848 +0 180.000000 +0 152 151 116 C 1.545000 +0 109.470848 +0 180.000000 +0 189 152 151 C 1.544986 +0 109.470848 +0 180.000000 +0 154 153 118 C 1.545000 +0 109.470848 +0 180.000000 +0 191 154 153 C 1.544986 +0 109.470848 +0 60.000000 +0 158 157 116 C 1.545000 +0 109.470848 +0 180.000000 +0 193 158 157 C 1.544986 +0 109.470848 +0 180.000000 +0 160 159 122 C 1.545000 +0 109.470848 +0 180.000000 +0 195 160 159 C 1.544986 +0 109.470848 +0 180.000000 +0 162 161 124 C 1.545000 +0 109.470848 +0 180.000000 +0 197 162 161 C 1.544986 +0 109.470848 +0 180.000000 +0 158 157 116 C 1.545000 +0 109.470848 +0 180.000000 +0 199 158 157 C 1.544986 +0 109.470848 +0 180.000000 +0 164 163 128 C 1.545000 +0 109.470848 +0 180.000000 +0 201 164 163 C 1.544986 +0 109.470848 +0 180.000000 +0 166 165 130 C 1.545000 +0 109.470848 +0 180.000000 +0 203 166 165 C 1.544986 +0 109.470848 +0 60.000000 +0 170 169 128 C 1.545000 +0 109.470848 +0 180.000000 +0 205 170 169 C 1.544986 +0 109.470848 +0 180.000000 +0 172 171 134 C 1.545000 +0 109.470848 +0 180.000000 +0 207 172 171 C 1.544986 +0 109.470848 +0 180.000000 +0 174 173 136 C 1.545000 +0 109.470848 +0 180.000000 +0 209 174 173 C 1.544986 +0 109.470848 +0 180.000000 +0 170 169 128 C 1.545000 +0 109.470848 +0 180.000000 +0 211 170 169 C 1.544986 +0 109.470848 +0 180.000000 +0 176 175 140 C 1.545000 +0 109.470848 +0 180.000000 +0 213 176 175 C 1.544986 +0 109.470848 +0 180.000000 +0 178 177 142 C 1.545000 +0 109.470848 +0 180.000000 +0 215 178 177 XX 2.522957 +0 90.000000 +0 90.000000 +0 11 6 5 XX 2.522957 +0 90.000000 +0 -90.000000 +0 31 26 25 XX 2.522957 +0 90.000000 +0 -90.000000 +0 187 146 145 Tv 10.70400010.704000 +1 0.000000 +0 0.000000 +0 1 217 2 Tv 10.70400010.704000 +0 0.000000 +0 0.000000 +0 1 218 2 Tv 10.70400010.704000 +0 0.000000 +0 0.000000 +0 1 219 2 2 19 1.914854 3 2 19 1.632993 13 2 19 6.928203 220 2 1 4 6 7 8 9 10 11 12 14 15 2 1 16 17 18 19 20 21 22 23 24 26 2 1 27 28 29 30 31 32 33 34 35 36 2 1 37 38 39 40 41 42 43 44 45 46 2 1 47 48 49 50 51 52 53 54 55 56 2 1 57 58 59 60 61 62 63 64 65 66 2 1 67 68 69 70 71 72 74 75 76 77 2 1 78 79 80 81 82 83 84 85 86 87 2 1 88 89 90 91 92 93 94 95 96 97 2 1 98 99 100 101 102 103 104 105 106 107 2 1 108 109 110 111 112 113 114 115 116 117 2 1 118 119 120 121 122 123 124 125 126 127 2 1 128 129 130 131 132 133 134 135 136 137 2 1 138 139 140 141 142 143 144 146 147 148 2 1 149 150 151 152 153 154 155 156 157 158 2 1 159 160 161 162 163 164 165 166 167 168 2 1 169 170 171 172 173 174 175 176 177 178 2 1 179 180 181 182 183 184 185 186 187 188 2 1 189 190 191 192 193 194 195 196 197 198 2 1 199 200 201 202 203 204 205 206 207 208 2 1 209 210 211 212 213 214 215 216 3 1 5 3 2 4 5 6 4 3 5 6 8 10 12 15 16 17 18 20 4 3 21 22 23 24 27 28 29 30 32 33 4 3 34 35 36 38 40 42 43 44 46 48 4 3 50 52 54 56 58 60 62 64 66 68 4 3 70 72 75 76 77 78 80 81 82 83 4 3 84 85 86 87 88 89 90 92 93 94 4 3 95 96 97 98 99 100 101 102 104 105 4 3 106 107 108 110 111 112 113 114 116 117 4 3 118 119 120 122 123 124 125 126 127 128 4 3 129 130 131 132 134 135 136 137 138 139 4 3 140 141 142 143 144 147 148 149 150 152 4 3 153 154 155 156 157 158 159 160 161 162 4 3 164 165 166 167 168 169 170 171 172 173 4 3 174 176 177 178 179 180 182 183 184 185 4 3 186 188 189 190 191 192 194 195 196 197 4 3 198 199 200 201 202 203 204 206 207 208 4 3 209 210 211 212 213 214 215 216 7 2 8 9 10 11 12 15 16 17 18 19 7 2 20 21 22 23 24 27 28 29 30 31 7 2 32 33 34 35 36 37 38 39 40 41 7 2 42 43 44 45 46 47 48 49 50 51 7 2 52 53 54 55 56 57 58 59 60 61 7 2 62 63 64 65 66 67 68 69 70 71 7 2 72 75 76 77 78 79 80 81 82 83 7 2 84 85 86 87 88 89 90 91 92 93 7 2 94 95 96 97 98 99 100 101 102 103 7 2 104 105 106 107 108 109 110 111 112 113 7 2 114 115 116 117 118 119 120 121 122 123 7 2 124 125 126 127 128 129 130 131 132 133 7 2 134 135 136 137 138 139 140 141 142 143 7 2 144 147 148 149 150 151 152 153 154 155 7 2 156 157 158 159 160 161 162 163 164 165 7 2 166 167 168 169 170 171 172 173 174 175 7 2 176 177 178 179 180 181 182 183 184 185 7 2 186 187 188 189 190 191 192 193 194 195 7 2 196 197 198 199 200 201 202 203 204 205 7 2 206 207 208 209 210 211 212 213 214 215 7 2 216 7 3 45 47 51 53 57 59 63 65 69 71 7 14 37 79 91 103 121 133 151 163 175 193 7 14 205 9 3 11 9 14 39 41 13 1 25 73 145 217 218 219 13 2 14 25 26 73 74 145 146 217 218 219 13 3 19 25 31 73 115 145 187 218 219 13 14 217 14 3 26 74 146 49 3 61 55 3 67 109 181 220 1 221 222 |
All distances are related by symmetry to the C1-C2 distance, here 1.545 Å. This means that the three unique distances, 2.958427, 2.522957, and 10.704000 Å, are related to the C1-C2 distance. If these three distances are defined using symmetry functions within MOPAC, then their optimization flags can also be set to zero. This can be done using internal coordinate symmetry-function 19. The resulting data set is shown in Figure 2. Note the three function 19 definitions at the start of the symmetry data. Within the automatically-generated symmetry data there are many references to symmetry functions 2 and 3 - these define angles and dihedral angles to be the same - but none of these angles are allowed to vary. These symmetry functions can be deleted or left in place; their presence or absence will not affect the calculation.
Diamond.mop can the be run using MOPAC to generate a BRZ file, Diamond.br. For convenience, this file should be renamed "Diamond for electronics.br" This prevents it accidentally getting overwritten in the event that Diamond.mop was re-run.
| Figure E2: Diamond Electronic
Band Structure Example of a "Walk" in k-space, from Excel |
|
 |
The Brillouin Zone for Diamond is a truncated octahedron. This structure has a high symmetry, so for ease of study, only the irreducible wedge need be examined. This wedge is defined by the six vertices (0,0,0), X (0.5,0,0), L (0.25,0.25,0.25),
| Point | Location | Description | Symmetry* |
| Γ | (0,0,0) | Center of BZ | Oh |
| X | (1/2,0,0) | Center of square face | ~D4h |
| L | (1/4,1/4.1/4) | Center of hexagonal face | ~(D3h and S6) |
| K | (3/8,3/8,0) | Center of edge of hexagonal face | C2v |
| W | (1/2,1/4,0) | Corner of a square face | ~S4 |
| U | (1/2,1/8,1/8) | Middle of edge of square face | C2v |
| *: "~" indicates no equivalent point-group,
the point-group(s) shown indicate some of the properties of the group. |
|||
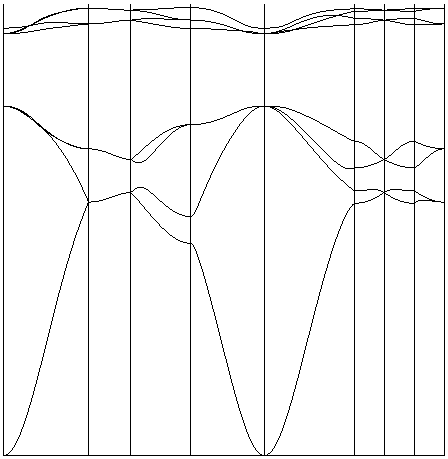
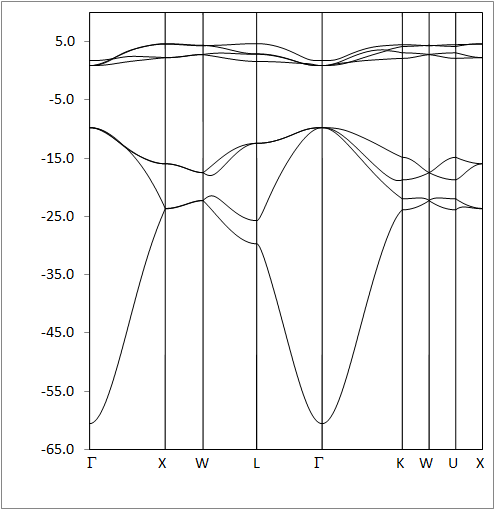
If "Diamond for electronics.brz" is opened using BZ, various walks in k-space can be generated. One of the more informative walks is Γ-X-W-L-Γ-K-W-U-X, shown in Figure E1. This figure, generated by BZ, is of some use (as shown here), but not easy to edit. When BZ is run, in addition to the simple graphic, it also produces a file that ends in ".txt" that contains all the information that was used in making the graphic. This information can then be using in Excel to make a chart that can easily be edited to add axes, text boxes, etc. An example is shown in Figure E2.
BZ can generate surfaces, these are square cross-sections through k-space. These cross-sections are defined by a point (three numbers) marking the center of the surface, a vector perpendicular to the surface (three numbers), and a distance (one number) from the point to the edge of the square. A single graphic can display only one energy band at a time.
An example of Band 1 is given in Figure E3, and of Band 2 in E4. As with a walk, these graphics, generated by the program BZ, are simple to make and to understand, but not easy to edit.
If the associated .txt file is used in Excel, other styles of display become available. Two examples of Band 1 at Γ are shown in Figures E5 and E6. In addition, as with the walks, these graphics can be annotated easily.
When a file containing the symmetry operations of the lattice are supplied, the symmetry properties of the eigenfunctions for individual points can be examined. An examination of the symmetry operations of the diamond lattice reveals that they map exactly onto the operations of the point-group Oh. Some points in the irreducible wedge have a symmetry exactly isomorphous with a point-group symmetry. For example the center of the Brillouin zone Γ has the same symmetry as point-group Oh. Other points, X is a good example, are unrelated to any point-group, although in the case of X, there is a superficial similarity to D4h. Other points, L being a good example, have a sub-group symmetry that maps to a point-group, here C3, but also has operations such as S6, C2 and I that look as if they belong to D6h, however the operation D6 is, of course, not present in the Oh point-group.
Finally, some points, although superficially different, are in fact related by a space-group symmetry operation, therefore the eigenvalues of the two points are the same and their associated eigenvectors have the same symmetry. This is seen in K and U, where, in addition to having the same little-group symmetry, that symmetry maps to the point-group C2v.
The vibrational or phonon Brillouin zone is constructed from the mass-weighted Hessian matrix for the Large Unit Cell. Within BZ, the behavior of the electronic and phonon energy matrices are almost the same, the only difference being the sizes of the matrices; the size of the electronic energy matrix is equal to the number of atomic orbitals, but in the phonon energy matrix the size is three times the number of atoms. Because of this similarity, working with the phonon Brillouin zone is exactly the same as working with the electronic Brillouin zone.
One dramatic difference between the appearances of the electronic and phonon Brillouin zones is the presence in the phonon structure of sharp points at Γ where the equivalent structure in the electronic Brillouin zone is of a local maximum or minimum. This is most dramatically seen in the Excel figures P3 and P4