Localization Theory

Various methods of localizing M.O.s have been proposed [61,62,63]. The method described here is a modification of Von Niessen's technique, and is ideally suited for semiempirical methods.

For a set of LMOs,

Σ_i<ψ_i⁴>

is a maximum. Since

Σ_iΣ_j<ψ_i²><ψ_i²>

is a constant,

Σ_iΣ_j<i<ψ_i²><ψ_i²>

must be a minimum.

The operation to localize M.O. consists of a series of binary unitary transforms of the type:

$\begin{displaymath}\vert\psi_i> =a\vert\psi_k> +b\vert\psi_l> \end{displaymath}$

$\begin{displaymath}\vert\psi_j> =-b\vert\psi_k> +a\vert\psi_l> \end{displaymath}$

where |ψ_k> and |ψ_l> are normal M.O.s, and |ψ_i> and |ψ_j> are the LMOs.

The ratio a/b is given by

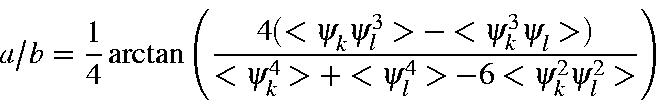
$\begin{displaymath}a/b = \frac{1}{4}\arctan\left(\frac{4(<\psi_k\psi_l^3>-<\psi_k^3\psi_l>)} {<\psi_k^4>+<\psi_l^4>-6<\psi_k^2\psi_l^2>}\right) \end{displaymath}$

Note that in normal semiempirical work: $<\phi_{\lambda}\vert\phi_{\sigma}> =\delta(\lambda,\sigma)$ .

From this it follows that, given $\psi_k = \sum_{\lambda}C_{\lambda k}\phi_{\lambda}$ ,

$\begin{displaymath}<\psi_k\psi_l^3> = \sum_{\lambda}C_{\lambda k}C_{\lambda l}^3 \end{displaymath}$

In order to preserve rotational invariance, all contributions on each atom must be added together. This gives:

$\begin{displaymath}<\psi_k^4> = \sum_A(\sum_{\lambda\in A}C_{\lambda k}^2)^2 \end{displaymath}$ ,

$\begin{displaymath}<\psi_k^3\psi_l> = \sum_A(\sum_{\lambda\in A}C_{\lambda k}^2) \sum_{\lambda\in A}C_{\lambda k}C_{\lambda l}\end{displaymath}$ ,

and

$\begin{displaymath}<\psi_k^2\psi_l^2> = \sum_A(\sum_{\lambda\in A}C_{\lambda k}^2)(\sum_{\lambda\in A}C_{\lambda l}^2) \end{displaymath}$

Number of Centers

The value of 1/<ψ⁴> is a direct measure of the number of centers involved in the MO: thus, the value of 1/<ψ⁴> is 2.0 for H₂, 3.0 for a three-center bond and 1.0 for a lone pair. There is no upper limit to the number of centers that can be in a localized M.O., although there are seldom more than 3 in any system. To understand this, consider a hypothetical system of 10 atoms that forms a perfect decagon, and each atom has only one atomic orbital, and the system has only one M. O. occupied. Okay, this is a ridiculous system, but it is being used for illustration only. The LMO and M.O., Ψ, would be the same:

Ψ = Σ_ic_iφ_i = Σ_i10^-½φ_i

The value of <Ψ⁴> would be

<Ψ⁴> = Σ_ijkl<c_iφ_ic_jφ_jc_kφ_kc_lφ_l>

which, because of orthonormality of the atomic orbitals in semiempirical methods would simplify to

<Ψ⁴> = Σ_ikc_i²<φ_iφ_i>c_k²<φ_kφ_k>

<Ψ⁴> = Σ_ik10^-1x10^-1δ(i,k) = 0.1

So the LMO would involve 10.0 centers.

Bonding contribution of each M.O.

The RHF bond-order matrix, P_λσ, is constructed using the occupied set of M.O.s:

P_λσ, = 2Σ_{i (occ)} c_λic_σi

so the atomic orbital contribution of localized M.O. "j" to bonding, B_jj, of each LMO is given by:

B_jj = 2Σ_λΣ_σc_λjc_σj2Σ_{i (occ)} c_λic_σi

Where λ and σ in the first two summations exclude all matrix elements involving the same atom. (Remember - bonds involve pairs of atoms.)

This summation can be re-cast in simpler form as:

B_jj = 2Σ_λΣ_σc_λjc_σjP_λσ

Note 1: The sum of the bonding contributions over all M.O.s (occupied plus virtual) is zero.

Note 2: A bonding M.O. will contribute ca. 2.0 to the bond-orders; a lone-pair will contribute ca. 0.0.