States

Calculating the characters for electronic states is much more complicated than that for M.O.s or normal coordinates.

Consider the effect of an operation, R, on a state, Φa. The character of the operation is given by

\begin{displaymath}\chi_{R,a} = <\Phi_a\vert R\vert\Phi_a>. \end{displaymath}

A state function can be expressed as a linear combination of microstates:

\begin{displaymath}\Phi_a = \sum_jC_{ja}\Psi_j, \end{displaymath}

so the character of the operation on the state function can be written in terms of microstates as

\begin{displaymath}\chi_{R,a} =\sum_i\sum_jC_{ia}C_{ja}<\Psi_i\vert R\vert\Psi_j>. \end{displaymath}

Each microstate, Ψj, can be represented by a Slater determinant of N molecular orbitals :

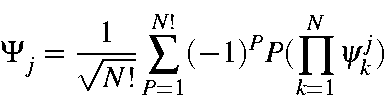
\begin{displaymath}\Psi_j = \frac{1}{\sqrt{N!}}\sum_{P=1}^{N!}(-1)^PP(\prod_{k=1}^N\psi_k^j) \end{displaymath}

where the molecular orbitals in the microstate consist of a selection of the M.O.s in the active space. Before we continue, let us examine this idea:

Consider a full set of M.O.s:

\begin{displaymath}\psi_1\psi_2\psi_3\psi_4 \psi_5 \psi_6 \psi_7 \psi_8 \psi_9 \psi_{10}\psi_{11}\psi_{12}\psi_{13}\psi_{14}\psi_{15}\psi_{16}. \end{displaymath}

Let the active space be the M.O.s from 8 to 11. Then microstates containing two electrons would be:
$\psi_8\psi_9$ $\psi_8\psi_{10}$ $\psi_8\psi_{11}$ $\psi_9\psi_{10}$ $\psi_9\psi_{11}$ $\psi_{10}\psi_{11}$.
These microstates could be represented by M.O. orbital occupancies.
1100    1010    1001    0110    0101    0011.
Remember that the M.O.s here can be of either α or β spin.

To continue, we need to evaluate $<\Psi_i\vert R\vert\Psi_j>$. This can be expressed in terms of M.O.s as:

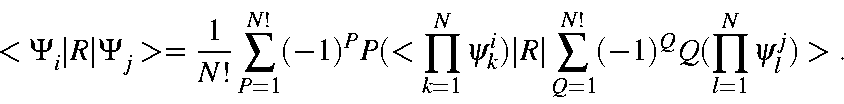
\begin{displaymath}<\Psi_i\vert R\vert\Psi_j> = \frac{1}{N!}\sum_{P=1}^{N!}(-1)^... ...i)\vert R\vert \sum_{Q=1}^{N!}(-1)^QQ(\prod_{l=1}^N\psi_l^j)>. \end{displaymath}

For convenience, we will represent the integral $<\psi_k^i\vert R\vert\psi_l^j>$ by $\chi_{kl}^{ij}$. This integral can be described as "The integral over M.O. ψk in microstate Ψi with the result of operator R acting on M.O. ψk in microstate Ψj.

Using this abbreviation, $<\Psi_i\vert R\vert\Psi_j>$ can be written as:

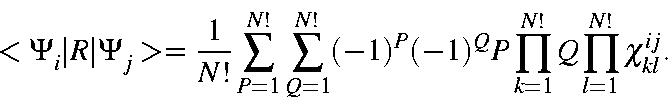
\begin{displaymath}<\Psi_i\vert R\vert\Psi_j> =\frac{1}{N!}\sum_{P=1}^{N!} \sum_... ...(-1)^P(-1)^Q P\prod_{k=1}^{N!}Q\prod_{l=1}^{N!}\chi_{kl}^{ij}. \end{displaymath}

Although it is not immediately obvious, the right-hand term is a determinant, of order N:

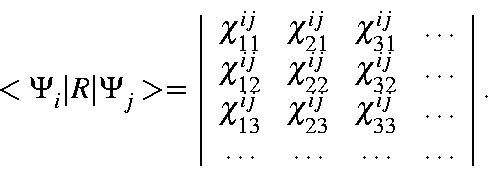
\begin{displaymath}<\Psi_i\vert R\vert\Psi_j> =\left\vert \begin{array}{cccc} \c... ...\ \ldots & \ldots & \ldots & \ldots \end{array}\right\vert. \end{displaymath}

For our purposes, solution of the determinant is best done explicitly. To see why, note that the number of M.O.s involved in the C.I. (the active space) is very small. Because of this, the number of electrons, N, in the Slater determinants is also small; N has a maximum value of 20. Next, use can be made of the fact that no point-group operation can mix α and β electrons. This allows the integral to be split into two parts, each of which has a maximum value of N=10. Finally, remember that N is the number of electrons, not M.O.s, used in the active space. A system of N electrons has the same symmetry as a system in which all the M.O.s which were occupied were replaced with all the M.O.s which were not occupied (the positron equivalent) . (This assumes that if every M.O. were occupied, then the state of the system would be totally symmetric.) Using this fact, we can replace the N occupied M.O.s with N' unoccupied M.O.s, if N' < N.

When these three points are considered, we see that N has a maximum value of 5 (for a system of 10 M.O.s). Each case can be considered separately.

For N = 1:

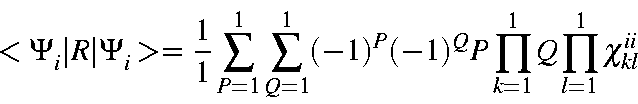
\begin{displaymath}<\Psi_i\vert R\vert\Psi_i> = \frac{1}{1}\sum_{P=1}^{1} \sum_{... ...{1}(-1)^P(-1)^Q P\prod_{k=1}^{1}Q\prod_{l=1}^{1}\chi_{kl}^{ii} \end{displaymath}

or

\begin{displaymath}<\Psi_i\vert R\vert\Psi_i> = <\psi_1^i\vert R\vert\psi_1^i> = \chi_{11}^{ii}. \end{displaymath}

For N=2:

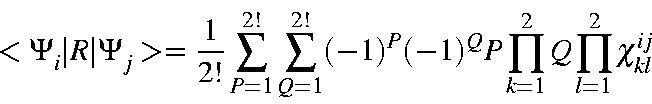
\begin{displaymath}<\Psi_i\vert R\vert\Psi_j> = \frac{1}{2!}\sum_{P=1}^{2!} \sum... ...2!}(-1)^P(-1)^Q P\prod_{k=1}^{2}Q\prod_{l=1}^{2}\chi_{kl}^{ij} \end{displaymath}

or

\begin{displaymath}<\Psi_i\vert R\vert\Psi_j> = <\psi_1^i\vert R\vert\psi_1^j>-<... ...> <\psi_1^i\vert R\vert\psi_2^j><\psi_1^i\vert R\vert\psi_2^j> \end{displaymath}

or

\begin{displaymath}<\Psi_a\vert R\vert\Psi_a> = \chi_{11}^{ij}\chi_{22}^{ij}-\chi_{12}^{ij}\chi_{21}^{ij}. \end{displaymath}

For N=3:

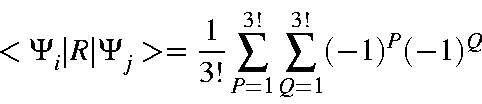
\begin{displaymath}<\Psi_i\vert R\vert\Psi_j> = \frac{1}{3!}\sum_{P=1}^{3!} \sum_{Q=1}^{3!}(-1)^P(-1)^Q \end{displaymath}


$\displaystyle <\Psi_i\vert R\vert\Psi_j>$ = $\displaystyle \ <\psi_1^i\vert R\vert\psi_1^j><\psi_2^i\vert R\vert\psi_2^j><\psi_3^i\vert R\vert\psi_3^j>$  
    $\displaystyle -<\psi_1^i\vert R\vert\psi_1^j><\psi_2^i\vert R\vert\psi_3^j><\psi_3^i\vert R\vert\psi_2^j>$  
    $\displaystyle -<\psi_1^i\vert R\vert\psi_2^j><\psi_2^i\vert R\vert\psi_1^j><\psi_3^i\vert R\vert\psi_3^j>$  
    $\displaystyle +<\psi_1^i\vert R\vert\psi_2^j><\psi_2^i\vert R\vert\psi_3^j><\psi_3^i\vert R\vert\psi_1^j>$  
    $\displaystyle +<\psi_1^i\vert R\vert\psi_3^j><\psi_2^i\vert R\vert\psi_1^j><\psi_3^i\vert R\vert\psi_2^j>$  
    $\displaystyle -<\psi_1^i\vert R\vert\psi_3^j><\psi_2^i\vert R\vert\psi_2^j><\psi_3^i\vert R\vert\psi_1^j>$  

or
$\displaystyle <\Psi_i\vert R\vert\Psi_j>$ = $\displaystyle \chi_{11}^{ij}\chi_{22}^{ij}\chi_{33}^{ij}+ \chi_{12}^{ij}\chi_{23}^{ij}\chi_{31}^{ij}+ \chi_{13}^{ij}\chi_{21}^{ij}\chi_{32}^{ij}$  
    $\displaystyle -\chi_{11}^{ij}\chi_{23}^{ij}\chi_{32}^{ij} -\chi_{12}^{ij}\chi_{21}^{ij}\chi_{33}^{ij} -\chi_{13}^{ij}\chi_{22}^{ij}\chi_{31}^{ij}).$  

For higher numbers of electrons, the associated determinant is solved using standard methods.

The total character, $<\Psi_a\vert R\vert\Psi_a>$, is obtained by multiplying the characters for the $\alpha$ and $\beta$ parts together:

\begin{displaymath}<\Psi_a\vert R\vert\Psi_a> = <\Psi_a^{\alpha}\vert R\vert\Psi_a^{\alpha}> <\Psi_a^{\beta}\vert R\vert\Psi_a^{\beta}>. \end{displaymath}

If the positron equivalent is taken for only one set of electrons, e.g. either the α or the β set, but not both, then the character has to be multiplied by the determinant of the M.O. transform.

These expressions can then be used in

\begin{displaymath}\chi_{R,a} =\sum_i\sum_jC_{ia}C_{ja}<\Psi_i\vert R\vert\Psi_j>. \end{displaymath}

to give the expectation value for the state. Finally, if the state is degenerate, the character is given by summing the components of the state.

For the atom, the Russell-Saunders coupling scheme can be reproduced. States allowed are S, P, D, F, G, H, I, K, L, and M. This set is more than sufficient to allow all possible Russell-Saunders states spanned by a basis set of s, p, and d orbitals to be represented. The highest angular momentum achievable with such a basis set is 8, i.e. L. For simpler atoms (ones with only a s-p basis set) the allowed states are p0,p6: 1Sg,   p1,p5: 2Pu,   p2,p4: 1Sg+3Pg+1Dg ,   p3: 4Su+2Pu+2Du.

For the axial infinite groups, allowed states are: Σ, Π, Δ, θ, and Γ. Even quite simple systems can achieve quite high angular momentum, thus acetylene, with a C.I.=4 (the HOMO π and LUMO π*) will contain a 1Γg state, i.e., the angular momentum will be 4.

At present J-J coupling is not supported.