Construction of secular determinant

Microstates can be generated by permuting available electrons among the available levels. Elements of the C.I. matrix are then defined by

<Ψa |H|Ψb>

Evaluation of these matrix elements is difficult. Each microstate is a Slater determinant, and the Hamiltonian operator involves all electrons in the system. Fortunately, most matrix elements are zero because of the orthogonality of the M.O.s. Only the non-zero elements need be evaluated; three types of interaction are possible:
1. Ψa = Ψb. Since the two wavefunctions are the same, this corresponds to the energy of a microstate. As the electronic energy of the closed shell is common to all configurations considered in the C.I., it is sufficient to add on to Eg+ the energy terms which are specific to the microstate, thus
=
   

2. Except for ψi in Ψa and ψj in Ψb; Ψa = Ψb. Assuming ψi and ψj to be α-spin the interaction energy is

\begin{displaymath}<\Psi_a\vert H\vert\Psi_b> = (-1)^W(\epsilon_{ij}^++\sum_{k=B... ...t kk>-<ik\vert jk>)O_k^{\alpha a} +<ij\vert kk>O_k^{\beta a}). \end{displaymath}

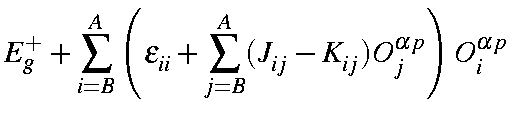
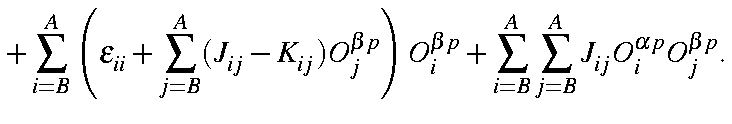This presents a problem. Unlike $\epsilon_{ii}^+$, which has already been defined, there is no easy way to calculate $\epsilon_{ij}^+$. Rather than undertake this calculation, use can be made of the fact that, for the starting configuration:

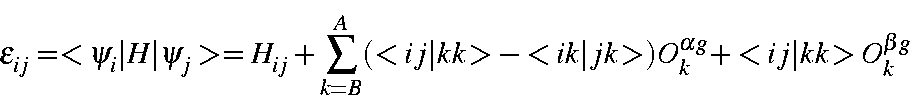
\begin{displaymath}\epsilon_{ij} = <\psi_i\vert H\vert\psi_j> = H_{ij} + \sum_{... ...t kk>-<ik\vert jk>)O_k^{\alpha g} +<ij\vert kk>O_k^{\beta g} \end{displaymath}

or

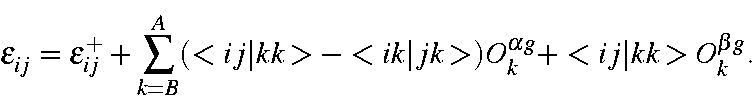
\begin{displaymath}\epsilon_{ij} = \epsilon_{ij}^+ + \sum_{k=B}^A(<ij\vert kk>-<ik\vert jk>)O_k^{\alpha g} +<ij\vert kk>O_k^{\beta g} . \end{displaymath}

$\epsilon_{ij}$ corresponds to an off-diagonal term in the Fock matrix, which at self-consistency is, by definition, zero. Therefore:

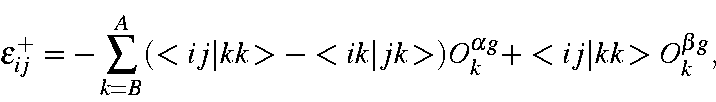
\begin{displaymath}\epsilon_{ij}^+ = - \sum_{k=B}^A(<ij\vert kk>-<ik\vert jk>)O_k^{\alpha g} +<ij\vert kk>O_k^{\beta g} , \end{displaymath}

which can be substituted directly into the expression for $<\Psi_a\vert H\vert\Psi_b>$ to give

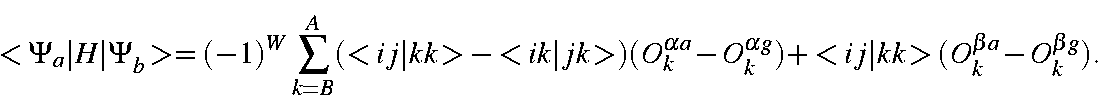
\begin{displaymath}<\Psi_a\vert H\vert\Psi_b> = (-1)^W\sum_{k=B}^A(<ij\vert kk>-... ...O_k^{\alpha g}) +<ij\vert kk>(O_k^{\beta a} -O_k^{\beta g} ). \end{displaymath}

All that remains is to determine the phase factor. One of the microstates is permuted until the two unmatched M.O.s occupy the same position. The number of permutations needed to do this when the two M.O.s are of $\alpha$ spin is

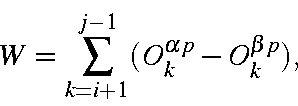
\begin{displaymath}W=\sum_{k=i+1}^{j-1}(O_k^{\alpha p}-O_k^{\beta p}), \end{displaymath}

assuming j > i; otherwise:

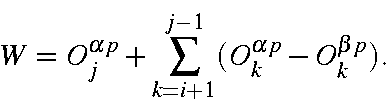
\begin{displaymath}W=O_j^{\alpha p} +\sum_{k=i+1}^{j-1}(O_k^{\alpha p}-O_k^{\beta p}). \end{displaymath}

3. Except for ψi and ψj in Ψa and ψk and ψl in Ψb; Ψa = Ψb. Two situations exist: (a) when all four M.O.s are of the same spin; and (b) when two are of each spin. Thus,
(a) All four M.O.s are of the same spin. The interaction energy is

\begin{displaymath}<\Psi_a\vert H\vert\Psi_b> = (-1)^W[<ik\vert jl>-<il\vert jk>], \end{displaymath}

in which the phase factor is:

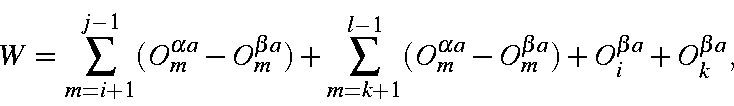
\begin{displaymath}W=\sum_{m=i+1}^{j-1}(O_m^{\alpha a}-O_m^{\beta a}) + \sum_{m=... ...}(O_m^{\alpha a}-O_m^{\beta a})+O_i^{\beta a} + O_k^{\beta a}, \end{displaymath}

if the four M.O.s are of α spin; otherwise,

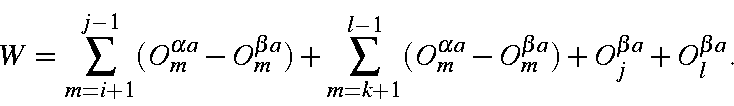
\begin{displaymath}W=\sum_{m=i+1}^{j-1}(O_m^{\alpha a}-O_m^{\beta a}) + \sum_{m... ...}(O_m^{\alpha a}-O_m^{\beta a})+O_j^{\beta a} + O_l^{\beta a}. \end{displaymath}

(b) Two M.O.s are of each spin. In this case there is no exchange integral, therefore the interaction energy is

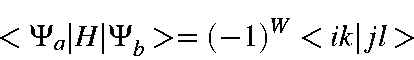
\begin{displaymath}<\Psi_a\vert H\vert\Psi_b> = (-1)^W<ik\vert jl> \end{displaymath}

and the phase factor is:

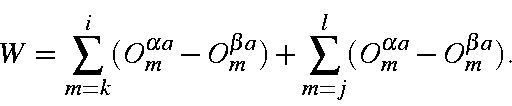
\begin{displaymath}W=\sum_{m=k}^{i}(O_m^{\alpha a}-O_m^{\beta a}) + \sum_{m=j}^{l}(O_m^{\alpha a}-O_m^{\beta a}). \end{displaymath}

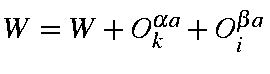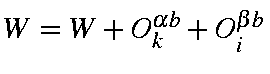If i > k, then $W=W+O_k^{\alpha a}+O_i^{\beta a}$, if j > l, then $W=W+O_k^{\alpha b}+O_i^{\beta b}$, finally, if i > k and j > l or i < k and j < l, then W=W+1.

All other matrix elements are zero. The completed secular determinant is then diagonalized. This yields the    state vectors and state energies, relative to the starting configuration. In turn, the state vectors can be used to generate spin density (at the RHF level) for pure spin states. If the density matrix for the state is of interest, such as in the calculation of transition dipoles for vibrational modes of excited or open shell systems, or for other use, the perturbed density matrix is   reconstructed.