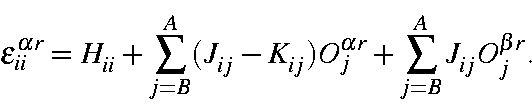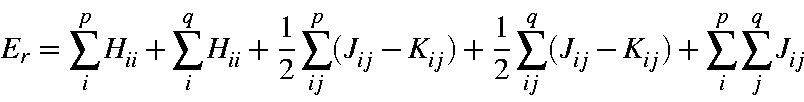
The electronic energy, Er, of any microstate Ψr is the sum on the one and two-electron energies:
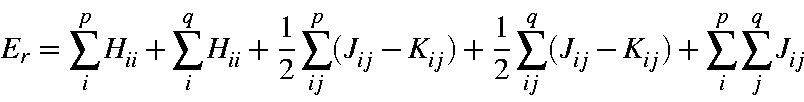
where Hii is the one-electron energy of M.O. ψi, Jii is the two-electron Coulomb integral <ψiψi|ψjψj>, and Kii is the two-electron exchange integral <ψiψj|ψiψj>. In this section it is more convenient to express it in terms of molecular orbital occupancies:
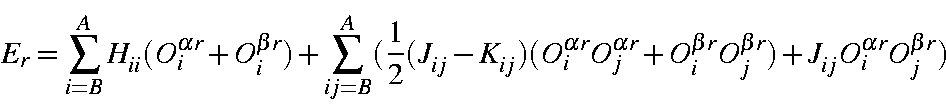
Similarly, the orbital energies can be written
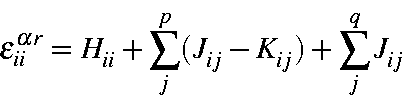
or, in terms of orbital occupancies