Test of DRC--verification of trajectory path

Introduction: Unlike a single-geometry calculation or even a geometry optimization, verification of a DRC trajectory is not a simple task. In this section a rigorous proof of the DRC trajectory is presented; it can be used both as a test of the DRC algorithm and as a teaching exercise. Users of the DRC are asked to follow through this proof in order to convince themselves that the DRC works as it should.

The nitrogen molecule

For the nitrogen molecule (using MNDO) the equilibrium distance is 1.103816Å, the heat of formation is 8.25741 kcal/mol and the vibrational frequency is 2738.8 cm-1. For small displacements, the energy curve versus distance is parabolic and the gradient curve is approximately linear, as is shown in the Table. A nitrogen molecule is thus a good approximation to a harmonic oscillator.


 

Table:

 Stretching Curve for Nitrogen Molecule

N-N DIST

$Delta H_f$

GRADIENT

(Ångstroms)

(kcal/mol)

(kcal/mol/Ångstrom)

1.11800

8.69441

60.84599

1.11700

8.63563

56.70706

1.11600

8.58100

52.54555

1.11500

8.53054

48.36138

1.11400

8.48428

44.15447

1.11300

8.44224

39.92475

1.11200

8.40444

35.67214

1.11100

8.37091

31.39656

1.11000

8.34166

27.09794

1.10900

8.31672

22.77620

1.10800

8.29611

18.43125

1.10700

8.27986

14.06303

1.10600

8.26799

9.67146

1.10500

8.26053

5.25645

1.10400

8.25749

0.81794

1.10300

8.25890

-3.64427

1.10200

8.26479

-8.12993

1.10100

8.27517

-12.63945

1.10000

8.29007

-17.17278

1.09900

8.30952

-21.73002

1.09800

8.33354

-26.31123

1.09700

8.36215

-30.91650

1.09600

8.39538

-35.54591

1.09500

8.43325

-40.19953

1.09400

8.47579

-44.87745

1.09300

8.52301

-49.57974

1.09200

8.57496

-54.30648

1.09100

8.63164

-59.05775

1.09000

8.69308

-63.83363




Period of vibration

The period of vibration (time taken for the oscillator to undertake one complete vibration, returning to its original position and velocity) can be calculated in three ways. Most direct is the calculation from the energy curve; using the gradient constitutes a faster, albeit less direct, method, while calculating it from the vibrational frequency is very fast but assumes that the vibrational spectrum has already been calculated.

1.
From the energy curve. For a simple harmonic oscillator the period r is given by:

\begin{displaymath}r = 2 \pi \sqrt{\frac{\mu}{k}} \end{displaymath}


where k is the force constant. The reduced mass, μ, (in amu) of a nitrogen molecule is 14.0067/2 = 7.00335, and the force-constant, k, can be calculated from:

E-c = (1/2) k(R-Ro)2.


Given Ro = 1.1038, R = 1.092, c = 8.25741 and E = 8.57496 kcal/mol then:

k = 2x0.31755/(0.0118)2 (per mole)

k = 4561.2 kcal/mol/A2 (per mole)

k = 1.9084x1030 ergs/cm2 (per mole)

k = 31.69x105 dynes/cm (per molecule)

(Experimentally, for N2, k = 23x105 dynes/cm )


Therefore:

\begin{displaymath}r = 2 \times 3.14159 \times \sqrt{\frac{7.0035}{1.9084\times ... ...seconds} = 12.037 \times 10^{-15}\;{\rm s} = 12.037\;{\rm fs}. \end{displaymath}


If the frequency is calculated using the other half of the curve ( R=1.118, E=8.69441), then k=12.333 fs, or k, average, = 12.185 fs.

2.
From the gradient curve. The force constant is the derivative of the gradient wrt distance:

\begin{displaymath}k = \frac{dG}{dx}. \end{displaymath}


Since we are using discrete points, the force constant is best obtained from finite differences:

\begin{displaymath}k = \frac{(G_2-G_1)}{(x_2-x_1)}. \end{displaymath}


For x2 = 1.1100, G2 = 27.098 and for x1 = 1.0980, G1 = -26.311, giving rise to k = 4450.75 kcal/mol/Å2 and a period of 12.185 fs.

3.
From the vibrational frequency. Given a "frequency" (wavenumber) of vibration of N2 of ν = 2738.8 cm-1, the period of oscillation, in seconds, is given directly by:

\begin{displaymath}r = \frac{1}{c\bar{\nu}} = \frac{1}{2738.8 \times 2.998 \times 10^{10}} ,\end{displaymath}


or as 12.179 fs.

Summarizing, by three different methods the period of oscillation of N2 is calculated to be 12.1851, 12.185 and 12.179 fs, average 12.183 fs.


Initial dynamics of N2 with N-N distance = 1.094 Å

A useful check on the dynamics of N2 is to calculate the initial acceleration of the two nitrogen atoms after releasing them from a starting interatomic separation of 1.094 Å.

At R(N-N) = 1.094 Å, G = -44.877 kcal/mol/Å or 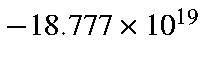$-18.777 \times 10^{19}$ erg/cm. Therefore acceleration, 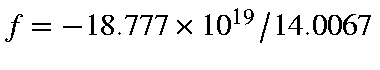$f = -18.777 \times 10^{19} /14.0067$ cm/sec/sec, or 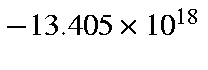$-13.405 \times 10^{18}$ cm/s2, which is 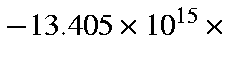$ -13.405 \times 10^{15} \times$ Earth surface gravity.

Distance from equilibrium = 0.00980 Å. After 0.1 fs, velocity is 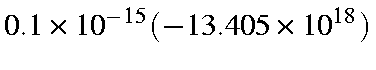$0.1\times 10^{-15} (-13.405 \times 10^{18})$ cm/sec or 1340.5 cm/s.

In the DRC the time-interval between points calculated is a complicated function of the curvature of the local surface. By default, the first time-interval is 0.105fs, so the calculated velocity at this time should be 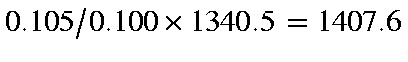$0.105/0.100 \times 1340.5 = 1407.6$ cm/s, in the DRC calculation the predicted velocity is 1407.6 cm/s.

The option is provided to allow sampling of the system at constant time-intervals, the default being 0.1 fs. For the first few points the calculated velocities are given in Table 1.


  Table 1: Velocities in DRC for N2 Molecule
Time Calculated Linear Diff. in
  Velocity Velocity Velocity
0.000 0.0 0.0 0.0
0.100 1340.6 1340.5 -0.1
0.200 2678.0 2681.0 -3.0
0.300 4007.0 4021.5 -14.5
0.400 5325.3 5362.0 -36.7
0.500 6628.4 6702.5 -74.1
0.600 7912.7 8043.0 -130.3


As the calculated velocity is a fourth-order polynomial of the acceleration, and the acceleration, its first, second and third derivatives, are all changing, the predicted velocity rapidly becomes a poor guide to future velocities.

For simple harmonic motion the velocity at any time is given by:

\begin{displaymath}v = v_0 \sin(2\pi t/r). \end{displaymath}


By fitting the computed velocities to simple harmonic motion, a much better fit is obtained (Table 2).


  Table 2: Modified Velocities in DRC for N2 Molecule
  Calculated Simple Harmonic Diff.
Time Velocity 25325.Sin(0.5296t)  
0.000 0.0 0.0 0.0
0.100 1340.6 1340.6 0.0
0.200 2678.0 2677.4 +0.6
0.300 4007.0 4006.7 +0.3
0.400 5325.3 5324.8 +0.5
0.500 6628.4 6628.0 +0.4
0.600 7912.7 7912.5 0.0


The repeat-time required for this motion is 11.86 fs, in good agreement with the three values calculated using static models. The repeat time should not be calculated from the time required to go from a minimum to a maximum and then back to a minimum--only half a cycle. For all real systems the potential energy is a skewed parabola, so that the potential energy slopes are different for both sides; a compression (as in this case) normally leads to a higher force-constant, and shorter apparent repeat time (as in this case). Only the addition of the two half-cycles is meaningful.