MOZYME and Excited States

For most systems, a calculation run using the linear scaling method MOZYME will produce the same result as a calculation run using conventional SCF methods.  In some systems, however, a MOZYME calculation will result in a heat of formation that is significantly greater than that predicted using conventional methods.  The questions that come to mind are:

(A) Under what conditions would MOZYME produce a DH_f that is significantly greater than that predicted by conventional methods?
(C) What is the cause of the DH_f being different, depending on how the SCF equations are solved?
(D) What are the implications of the different DH_f?

 Discussion of why MOZYME sometimes produces a DH_f that is significantly greater than that predicted by conventional methods

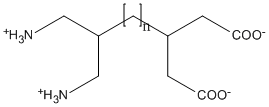
 Consider now the systems consisting of a number, n, of methylene groups forming a chain, at one end there is a doubly-ionized glutarate group, and at the other end is a doubly-ionized 1,3-diammino propyl group, see figure.  Single SCF calculations (1SCF) were run on each system using the conventional SCF calculation, call this MOPAC, and also using the MOZYME method of solving the SCF equations.  For small values of n, MOPAC gave the same result as a MOZYME calculation, see table headed "Gas-phase," but for larger values of n, the MOZYME results gave DH_f that were greater than the MOPAC results.  Unless a mistake is made, by definition, the lower the energy the better, so there is an apparent fault in the MOZYME results.

An examination of the charges on the atoms in the systems where the MOPAC and MOZYME results are different shows that in the MOPAC results the net charge on the diammine end converges on  +1.0 as n increases, while the MOZYME charge stays at ca. +2.0.  A similar trend occurs at the di-carboxylate end, where the MOPAC charge converges on -1.0 and the MOZYME charge stays at ca. -2.0. The effect of the charged ends is also reflected in the dipole moments.  For n=10, these are 97.5D (MOPAC) and 151.7D (MOZYME).

The systems being used are, however, very artificial.  In the MOPAC calculations, the energy can be lowered by forming a radical, where two of the electrons on the di-carboxylate end are moved to the diammine end of the molecule.  That this occurs can be verified by running a UHF calculation on the various systems.  Where the MOPAC and MOZYME results agree, the <S²> is zero, where they differ, the <S²> is non-zero.

Does this represent a fault or limitation of the MOZYME method?  In short, the answer is no, for several reasons:

• The completely artificial nature of the systems described here - highly ionic, gas-phase species - never occurs naturally.  The species were deliberately selected to illustrate the issue described here.
• If an ionic organic system can be stabilized by forming a radical, the system must necessarily be of high energy. Such a system could be more easily stabilized by migration of protons, thus neutralizing the charges.
• While the MOPAC result is better, in that the energy is lower than the MOZYME result, the energy can be still further decreased by running the calculation using the UHF method. The MOPAC RHF result is thus not the correct minimum, albeit it is better than the MOZYME result.
• The MOZYME result can be generated by a simple C.I. calculation starting with the MOPAC result, showing that both wavefunctions are stationary points in wavefunction space. 
• If the systems are stabilized by solvation using water, the MOPAC and MOZYME results agree for all values of n, see table headed "In water," illustrating the fact that the different results obtained using MOPAC and MOZYME were due to the highly artificial nature of the species.
• The conventional MOPAC method fails quite often when very exotic systems are modeled.  The MOZYME technique is more stable, and can frequently generate a SCF where MOPAC fails.

Archive files, that can be used as MOPAC data-sets, for MOPAC and MOZYME calculations in gas-phase and in solution can be downloaded.